請問巫師 #313
提醒其他讀者,埃及豔後基諾的玩法與傳統基諾類似,但如果最後抽出的球與玩家選擇的球之一匹配並獲勝,則玩家還將贏得12次免費遊戲,乘數為2倍。免費遊戲並不能獲得更多免費遊戲。
您沒有指定選號數或賠付表,所以我們以3-10-56-180-1000選號-8賠付表為例。首先,讓我們計算一下回報。
在基諾遊戲中,從 y 個球中接住 x 個球的方法數,就是從 20 個球中接住 x 個球,從 60 個球中接住 yx 個球的方法數。用 Excel 表達式表示,這等於 combin(20,x)*combin(60,yx)。再提醒一下,combin(x,y) = x!/(y!*(xy)!)。最終 x! = 1*2*3*...*x。
回顧完畢,以下是該賠付表的報酬率表。右列顯示的是預期贏利平方,我們稍後會用到。
選 8 基諾
| 事件 | 支付 | 組合 | 可能性 | 返回 | 返回^2 |
|---|---|---|---|---|---|
| 0 | 0 | 2,558,620,845 | 0.088266 | 0.000000 | 0.000000 |
| 1 | 0 | 7,724,138,400 | 0.266464 | 0.000000 | 0.000000 |
| 2 | 0 | 9,512,133,400 | 0.328146 | 0.000000 | 0.000000 |
| 3 | 0 | 6,226,123,680 | 0.214786 | 0.000000 | 0.000000 |
| 4 | 3 | 2,362,591,575 | 0.081504 | 0.244511 | 0.733533 |
| 5 | 10 | 530,546,880 | 0.018303 | 0.183026 | 1.830259 |
| 6 | 56 | 68,605,200 | 0.002367 | 0.132536 | 7.422014 |
| 7 | 180 | 4,651,200 | 0.000160 | 0.028882 | 5.198747 |
| 8 | 1000 | 125,970 | 0.000004 | 0.004346 | 4.345661 |
| 全部的 | 28,987,537,150 | 1.000000 | 0.593301 | 19.530214 |
接下來,我們來計算一下平均獎金。從上表可以看出,不計獎金的平均贏利為0.593301。在獎金中,玩家可以獲得12次雙倍免費旋轉。因此,獎金的預期贏利為2×12×0.593301 = 14.239212。
接下來,我們來計算一下贏得獎金的機率。如果玩家抓到四個數字,那麼第20個球是這四個數字之一的機率是4/20。一般來說,如果玩家抓到c個數字,那麼第20個球對中獎有幫助的機率是c/20。
贏得獎金的公式為:機率(第 4 組)*(4/20) + 機率(第 5 組)*(5/20) + 機率(第 6 組)*(6/20) + 機率(第 7 組)*(7/20) + 機率(第 8 組)*(8/20)。我們可以從上面的回報表中知道任何特定獲勝的機率。因此,贏得獎金的機率為:
0.081504*(4/20) + 0.018303*(5/20) + 0.002367*(6/20) + 0.000160*(7/20) + 0.000004*(8/20) = 0.021644。
透過贏得獎金的機率和平均獎金贏額,我們可以計算出獎金的回報為 0.021644 × 14.239212 = 0.308198。
我們不需要知道,但遊戲的整體回報是基礎遊戲的回報加上獎金的回報,等於 0.593301 + 0.308198 = 0.901498。
現在,讓我們開始討論實際的變異數。提醒一下,方差的一般公式是:
var(x + y) = var(x) + var(y) + 2*cov(x,y),其中 var 代表方差,cov 代表協方差。在這個遊戲中:
總變異數 = var(基礎遊戲)+ var(獎勵)+ 2*cov(基礎遊戲和獎勵)。
變異數的基本公式是 E(x^2) - [E(x)]^2。換句話說,就是預期贏利的平方減去預期贏利的平方。
話雖如此,我們先從基礎遊戲的變異數開始。還記得我之前說過,我們需要第一個表格中的預期贏利平方嗎?第一個表格的右下角單元格顯示預期贏利平方為 19.530214。我們已經知道預期贏利是 0.593301。因此,基礎遊戲的變異數為 19.530214 - 0.593301 2 = 19.178208。
接下來,我們來計算獎金的變異數(假設已經中獎)。為此,回想一下:
var(ax) = a 2 x,其中 a 為常數。
還記得 n 個隨機變數 x 的變異數是 nx。
也就是說,如果 x 是獎勵遊戲中的基礎贏利,那麼整個獎勵的變異數為 2 (2) × 12 (x)。由上文可知,基礎遊戲中單次旋轉(不計獎勵)的變異數為 19.178208。因此,假設已經獲得獎勵,則獎勵的變異數為 2 (2) × 12 (x) × 19.178208 = 920.554000。
然而,我們需要知道的是第一個球被抽出之前獎金的方差,包括根本沒有獎金的可能性。不,我們不能簡單地將獎金的變異數乘以中獎機率。相反,回想一下var(x) = E(x^2) - [E(x)]^2。我們將其重新排列如下:
E(x^2) = var(x) + [E(x)]^2
我們知道獎金的平均值和方差,因此獎金的預期贏利平方為 920.554000 + 19.178208 2 = 1123.309169。
因此,在抽出第一球之前,獎金贏取的預期平方是 prob(bonus) × E(x^2) = 0.021644 × 1123.309169 = 24.313239。
我們已經計算出,在第一球開球前,獎金的預期贏利為0.308198。因此,在第一球開球前,獎金的總體變異數為24.313239 - 0.308198 2 = 24.218253。
下一步是計算協方差。你可能會問:「為什麼基礎獎金和獎勵獎金之間存在相關性?」 這是因為最後一個抽出的球必須對獎金產生貢獻才能觸發獎勵。假設最後一球對獎金產生貢獻,平均獎金就會增加。提醒一下,貝葉斯條件機率公式如下:
P(A 已知 B) = P(A 和 B)/P(B)。
然後,假設最後一球被擊中,讓我們重新為基礎遊戲的回報表:
Pick 8 Keno 給最後一球擊中
| 事件 | 支付 | 組合 | 可能性 | 返回 |
|---|---|---|---|---|
| 0 | 0 | - | 0.000000 | 0.000000 |
| 1 | 0 | - | 0.000000 | 0.000000 |
| 2 | 0 | - | 0.000000 | 0.000000 |
| 3 | 0 | - | 0.000000 | 0.000000 |
| 4 | 3 | 472,518,315 | 0.753119 | 2.259358 |
| 5 | 10 | 132,636,720 | 0.211402 | 2.114019 |
| 6 | 56 | 20,581,560 | 0.032804 | 1.837010 |
| 7 | 180 | 1,627,920 | 0.002595 | 0.467036 |
| 8 | 1000 | 50,388 | 0.000080 | 0.080310 |
| 全部的 | 627,414,903 | 1.000000 | 6.757734 |
右下角單元格顯示,假設最後一球被擊中,平均勝利為 6.757734。
接下來,回想一下你在大學統計課上學到的內容:
cov(x,y) = exp(xy) - exp(x)*exp(y) 。
在我們的例子中,設 x = 基礎遊戲勝利,y = 獎勵勝利。我們先來計算 exp(xy)。
Exp(xy) = prob(贏得的獎金)*(贏得獎金時的平均基礎遊戲勝利)*average(獎金勝利) + prob(未贏得的獎金)*(未贏得獎金時的平均基礎遊戲勝利)*average(未贏得獎金時的平均獎金勝利)。 很容易得出 average(未贏得獎金時的平均獎金勝利) = 0,因此我們可以將其重寫為:
Exp(xy) = prob(贏得的獎金)*(贏得獎金後的平均基礎遊戲勝利)*平均值(贏得的獎金) =
0.021644 × 6.757734 × 14.239212 = 2.082719。我們已經解了 E(x) 和 E(y),因此協方差是:
cov(x,y) = exp(xy) - exp(x)*exp(y) = 2.082719 - 0.593301 × 0.308198 = 1.899865。
讓我們回到涉及協方差時的變異數總體方程式:
總變異數 = var(基礎遊戲) + var(獎勵) + 2*cov(基礎遊戲與獎勵) = 19.178208 + 24.218253 + 2×1.899865 = 47.196191。標準差為其平方根,即 6.869948。
好了,就這樣吧。這花了我好幾個小時,希望你滿意。
我在Wizard of Vegas論壇上提出並討論了這個問題。
我聽說,在美國,離婚率通常為50%,這個數字是用同一時期內離婚數量與結婚數量之比來計算的。是這樣嗎?您認為這種統計方法公平嗎?我對此表示懷疑,因為您研究的是短期內的離婚數量,而不是長期婚姻的數量。
如果人口和年齡分佈穩定,那麼如果離婚機率真的是 50%,那麼在樣本量較大的情況下,我們預計在任何給定的時間段內都會看到一起離婚與兩起結婚的比例。
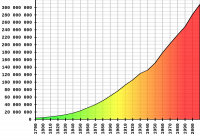
然而,人口並不穩定。從這張圖表來看,美國人口每十年增加10.71%,相當於每年1.02%。為了簡單起見,我們就假設是1%吧。
地圖來源:美國人口普查
據fatherly.com稱,失敗的婚姻平均持續 8 年。
如果您觀察到目前離婚與結婚的比例為 1 比 2,那麼任何特定婚姻以離婚告終的平均機率是多少?
我們現在看到的離婚案例是8年前結婚的,當時人口的比例是現在的92.35%。簡單的計算表明,真實的離婚機率是54.14%。
我們來檢查一下。
首先,根據疾病預防控制中心的數據,每年每1,000人中就有6.9對結婚。這個數字與本文的問題無關,但我認為有助於理解所涉及的數字。
假設8年前人口為3億,那麼當年結婚的人數為0.69%*3億=207萬對。
如果其中 54.14% 的人在八年後以離婚告終,那麼我們現在將看到 2,070,000 * 54.14% = 1,120,698 起離婚事件。
1,120,698 / 2,070,000 = 目前觀察到的離婚與結婚比率的 50%。
免得有人說,是的,我知道並非所有離婚都會在八年內結束。然而,綜合考慮,我認為最終結果與我54.14%的真實離婚率相差無幾。
這個問題是在我的「拉斯維加斯巫師」論壇中提出並討論的。
你的辦公室有100名員工,他們會舉辦一個秘密聖誕禮物交換活動。你會把每個人的名字寫在一張紙上,然後把紙放進一頂帽子裡,然後每個人隨機抽出一個名字作為禮物送給他們。
問題是,平均下來會有多少個閉環?比如說,戈登把錢給了唐,唐又給了喬恩,喬恩又給了內森,內森又給了戈登。或抽自己的名字。
假設每個人每次選擇一個。每個人選擇時,會出現兩種情況:
- 挑選者的名字已經被挑選出來了。
- 挑選者的名字仍然在名字箱裡。
對於任何給定的挑選者,假設還有 n 個人需要挑選。
如果正在挑選名字的人的名字已經被選中,那麼挑選者有 1/n 的機率會選擇與他名字相關的名字,從而形成一個閉環。例如,假設艾米正在挑選。艾米的名字已經被鮑伯佔據,鮑伯的名字已經被查理佔據,而查理的名字仍然在箱子裡。由於箱子裡還有 n 個名字,所以艾米選擇查理名字的機率為 1/n,從而形成一個閉環。
如果選擇者的名字尚未被選中,那麼艾米選擇自己名字的機率為 1/n,從而形成一個循環。
無論如何,如果拾取器沒有閉合一個環路,她就加入了另一條鏈的一部分,而這條鏈最終會被其他人閉合。每條鏈在閉合時只應計算一次。
因此答案是 1/100 + 1/99 + 1/98 + ... + 1/1 =~ 5.187377518。
對於任何足夠多的玩家數量 n 的估計值是 ln(n)。
這個問題是在我的Wizard of Vegas論壇中提出並討論的。
玩視訊老虎機時,額外的百搭保證值多少錢?
這取決於很多因素。我的理解是,如果一個額外的百搭符號比玩家通常獲得的平均數字高出多少,那麼它的價值是多少。雖然答案在不同遊戲中差異很大,但一個重要因素是螢幕上的行數。如果螢幕上有三行,額外的百搭符號將影響1/3的賠付線。同樣,如果螢幕上有四行,它的價值就會降低,影響1/4的賠付線。
為了回答你的問題,我研究了之前已經解構過的遊戲《埃及豔後》 。下表顯示了百搭符號的預期值相對於隨機百搭符號數量的成長情況。
埃及豔後中的額外狂野價值
| 捲軸 | 3 行 | 4 行 |
|---|---|---|
| 1 | 95.71% | 71.79% |
| 2 | 99.76% | 74.82% |
| 3 | 76.24% | 57.18% |
| 4 | 21.25% | 15.93% |
| 5 | 1.96% | 1.47% |