請問巫師 #270
輸的結果 = x*(100/750) = (2/15)x 設這些數字相等 50000-x = (2/15)x 50000 = (17/15)xx = 50000×(15/17) x = $44,117.65 看看這對不贏了，如果弗吉尼亞聯邦對減去希爾頓的賠付，再減去 Pinnacle 的 $44,117.65 = $5,882.35 如果弗吉尼亞聯邦大學輸了，希爾頓的賠付將一無所獲，但 Pinnacle 的賠付將達到 $44,117.65 × (100/750) = $5,882.35。不過，我懷疑押注維吉尼亞聯邦大學輸球的賠率是否公平。如果老闆極度厭惡風險，並且急於出售彩票，那麼我認為 6,000 美元左右的賠率比較公平。不過，我會根據維吉尼亞聯邦大學獲勝的賠率+604來計算他們的獲勝機率，這意味著獲勝機率為100/704 = 14.2%。這樣一來，這張彩券的價值就約為7,100美元。這還不包括稅收影響。這個問題是在我的配套網站 「拉斯維加斯巫師」（Wizard of Vegas）的論壇上提出並討論的。
（1）AAAAW/KK（W=百搭）
五張 A 在高牌中無人能敵，但一對 K 在低牌中卻可能打成平手。兩張 K 的組合數為combin (44,5) = 1,086,008。剩餘 46 張牌中，7 張牌的組合數總計為 53,524,680。因此，兩張 K 的機率為 1,086,008/53,524,680 = 2.03%。由於這些組合很多，莊家不會在低牌中打出 KK。根據我的牌九撲克附錄 1 ，莊家在高牌中拿到一對 A 或更小的牌的機率為 74.93%。這意味著他會組成兩對或更好的牌，這讓他有 25.07% 的機率在低牌中打出 K。因此，玩家獲得兩張 K 並能夠將其打出低牌的機率為 2.03% × 25.07% = 0.51%，即 196 分之一。
（2）AWQJT（同花）/AA
皇家牌可以與高牌打平，但 A 不能與低牌打平。這裡我用百搭牌代替 K 組成皇家牌，但它也可以代替 Q、J 或 T。我不想用它來代替 A，因為那樣一來牌堆裡就剩下兩張 A 讓莊家打平低牌了。這樣，莊家就只能用另一張皇家牌來與高牌打平。這種情況的幾率是多少？皇家牌剩下三種花色，另外兩張牌可以是任何花色。所以平手的組合數是 3×combin(41,2) = 2,460。玩家從原來的 43 張牌中拿走 7 張後，我從剩下的 46 張牌中得到 41 張，然後再減去莊家皇家牌中的 5 張牌中的 5 張。分母為 combin(46,7) = 53,524,680。因此，與 Wild Royal/AA 打平的機率為 2,460/53,524,680 = 0.004596%，即 21,758 分之一。
在某個完美主義者寫信給我之前，我可能會遇到一些奇怪的情況，例如荷官沒有按照我的意圖出牌。我的目的並非求出每種情況的確切機率，而是想證明為什麼我認為狂野皇家/AA 是牌九撲克中不莊牌時能拿到的最佳牌型。
這個問題是在我的同伴網站Wizard of Vegas的論壇中提出並討論的。
如果我們用基諾彩券來類比，每個人都有40個基因，每個基因都代表一個基諾球。然而，每個球都有一個唯一的編號。當兩個沒有血緣關係的人交配時，就像把他們兩人的80個球組合成一個漏斗，然後隨機選擇40個基因作為交配後代的基因。
所以，當你受孕時，你得到了一半的彩球，另一半則被浪費了。當你的兄弟姊妹受孕時，他/她得到了你出生時抽取的彩球的一半，以及另一半未被抽取的彩球。所以，你們的基因有50%是相同的。這和基諾彩券如果抽出40個號碼，連續兩次抽出平均會有20個相同的彩球的原因是一樣的。
這個問題是在我的同伴網站Wizard of Vegas的論壇中提出並討論的。
10把鋸子每小時鋸600分鐘。已知一張椅子鋸10分鐘，一張桌子鋸5分鐘。因此，每小時產量限制為：
（1）10c + 5t <= 600
6台車床每小時加工時間共360分鐘。我們已知，鋸一把椅子需要5分鐘，鋸一張桌子需要5分鐘。因此，每小時產量限制為：
（2）5c + 5t <= 360
18台砂光機每小時可進行1080分鐘的砂光作業。我們假設一張椅子需要鋸子5分鐘，一張桌子需要鋸子20分鐘。因此，每小時的產量限制為：
（3）5c + 20t <= 1080
下圖顯示了三組機器所施加的三個約束。工廠可以生產符合所有三條線的任意椅子和桌子組合。問題是，在三條線下，哪個組合能帶來最大的效益。
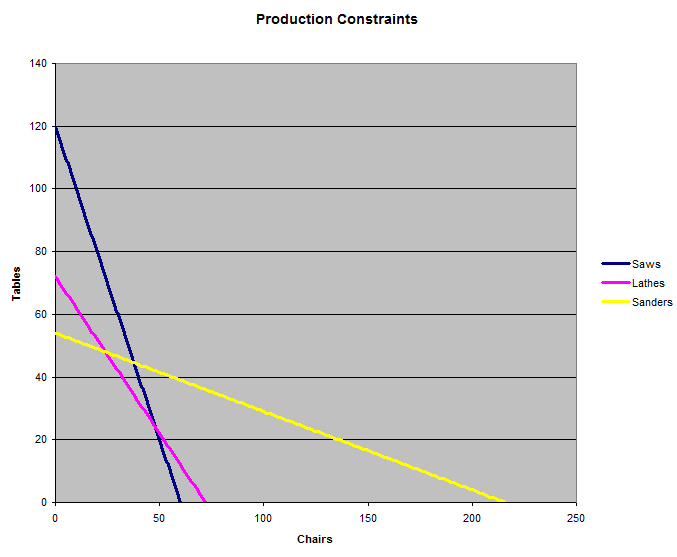
照理說，答案應該是兩條線的交點、所有椅子或所有桌子。那麼，讓我們找出這兩條線的交點。首先，讓我們找出公式 (1) 和公式 (2) 的交點。我們可以將 <= 表達式改為 =，以最大限度地發揮機器的潛力。
（1）10美分+5噸=600
（2）5c + 5t = 360
由 (1) 減去 (2)：
5美分=240
c = 48
將 48 代入公式 (1) 中，得到 c：
10×48 + 5t = 600
5t = 120
t = 24
因此，方程式 (1) 和 (2) 在 48 把椅子和 24 張桌子處相交。
接下來，讓我們找出方程式 (2) 和 (3) 的交點：
（2）5c + 5t = 360
（3）5c + 20t = 1080
從 (3) 減去 (2)：
15噸=720
t = 48
將其代入 (2) 或 (3) 中，我們可以解出 c，即 24。
因此，方程式 (2) 和 (3) 在 24 張椅子和 48 張桌子處相交。
我們不需要費心去尋找方程式 (1) 和 (3) 的交點，因為我們可以從圖中看到鋸線和砂光機線的交點在車床約束之外。
也可能只做椅子才是正確答案。圖表顯示，鋸子是只做椅子的最大限制因素。根據公式 (1)，如果我們將桌子數量代入 0，則 c=60。
另一種可能性是只做桌子。圖表顯示，砂磨機將是最大的限制因素。將0張椅子代入公式（3），我們發現最多只能做54張桌子。
下圖顯示了每個可行答案的總收入。記住，每張椅子的收入是10美元，每張桌子的收入是20美元。
每小時總收入
| 椅子 | 表格 | 收入 |
| 0 | 54 | 1,080美元 |
| 24 | 四十八 | 1,200美元 |
| 四十八 | 24 | 960美元 |
| 60 | 0 | 600美元 |