請問巫師 #267
如果您不確定答案,那麼在遊戲節目《百萬美元大灑千里》中分配資金的最佳策略是什麼?
為了其他讀者的利益,讓我先回顧一下規則。
- 一支球隊的起步資金為 1,000,000 美元。
- 團隊需要回答一道選擇題。
- 團隊要把錢分給所有可能的答案。所有投在正確答案上的錢都會進入下一個問題。
- 團隊必須完全排除至少一個可能的答案,不投入任何資金。
- 這個過程重複幾輪。玩家也有一次改變主意的機會。
顯然,如果團隊確定答案,那麼他應該把所有錢都押在正確答案上。如果團隊能把答案縮小到兩個,但每個答案都有50%的正確機率,那麼他們應該把錢平均分配給這兩個選項。
如果團隊傾向於某個答案,但又不完全排除其他一個或多個答案,情況就會變得更加困難。我們來看一個例子。假設團隊確定每個正確答案的機率如下:A 10%,B 20%,C 30%,D 40%。他們應該如何分配他的錢?
我認為答案是遵循凱利準則。簡而言之,團隊應該在每次提問時最大化其財富對數。要做到這一點,你必須考慮你已經擁有多少財富。
假設您現有的財富(獨立於節目本身累積)為 100,000 美元。這是您的第一個問題,因此您需要分配 1,000,000 美元的遊戲節目獎金。首先,排除機率最低的選項,以符合節目規則。然後,您需要最大化 0.2×log(100,000+b*1,000,000) + 0.3×log(100,000+c*1,000,000) + 0.4×log(100,000+d*1,000,000),其中小寫的比例分別代表每個分配的比例。
這可以用微積分和解三項式方程式、反覆試驗,或者我更喜歡用Excel的「目標搜尋」功能來解答。無論你用什麼方法,正確答案都是B佔18.9%,C佔33.3%,D佔47.8%。
當然,節目裡沒人能在規定時間內完成所有這些數學題,更別提你還得在這段時間內轉移一大堆現金。我更實際的建議是,根據你對答案正確機率的評估來分配資金,假設最不可能的選項不存在。在這個例子中,B選項分配22.2%,C選項分配33.3%,D選項分配44.4%。
這個問題是在我的同伴網站Wizard of Vegas的論壇中提出並討論的。
我聽過一家賭場,如果莊家爆牌,他會假定所有未出牌的玩家都贏了。遊戲發牌時牌面朝上,但雙倍下注的牌面朝下。所以,如果雙倍下注的牌導致玩家爆牌,而莊家也爆牌,那麼玩家就贏了。賭場這樣做是因為他們擔心算牌者,不想讓玩家看到他們認為無關緊要的牌。在這條規則下,正確的基本策略是什麼?賭場優勢又是什麼?
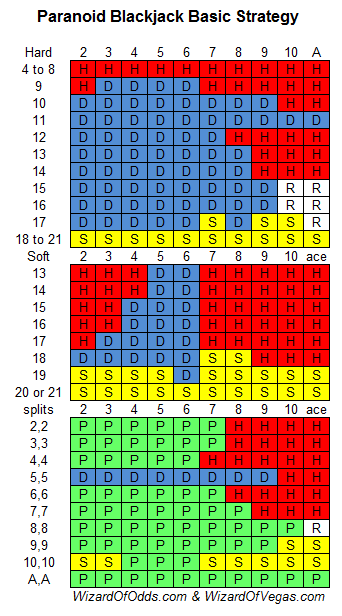
我假設有六副牌,莊家拿到軟17,分牌後加倍,投降,然後重新分牌。如果不允許小牌加倍,那麼我的玩家優勢是4.9%。這是正確的策略。顯然,這個策略可能會引發一些危險訊號。
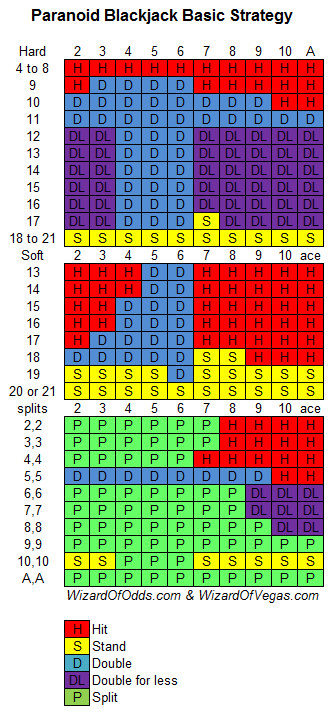
如果允許小額加倍,那麼我採用以下策略可以獲得最高9.4%的玩家優勢。小額加倍時,盡量少下注,最好只加一分錢。我的9.4%是基於小額加倍下注的假設。實際上,大多數賭場都要求至少達到賭桌最低投注額才能加倍。
這個問題是在我的同伴網站Wizard of Vegas的論壇中提出並討論的。
在維也納賭場,二十一點遊戲有附加賭注。遊戲使用六副牌,莊家在軟17點時停牌。如果莊家爆牌,無論原始賭注結果如何,賠率為2賠5。
我的二十一點附錄2B就是為這類問題而寫的。它顯示,在這些規則下,莊家爆牌的機率是28.19%。也就是說,賭場優勢是1.33%。
這個問題是在我的同伴網站Wizard of Vegas的論壇中提出並討論的。
您在2010年12月14日的專欄中寫道,賭場特別提到的「AAAAAKK」牌型在撲克歷史上可能從未出現過。據另一位荷官說,一位玩家在2010年11月在主街車站(Main Street Station)拿到了這手牌。
有意思。我之前寫過,我估計內華達州每23.7年就會出現一次這種手。我想那次就是其中一次。


