請問巫師 #265
我試用了你們的精算計算器。為什麼我達到預期死亡年齡的機率不到 50%?
你混淆了平均值和中位數。我們以我的情況為例。我是45歲的男性。我的預期壽命是78.11歲,但我活到80歲的機率是50.04%。
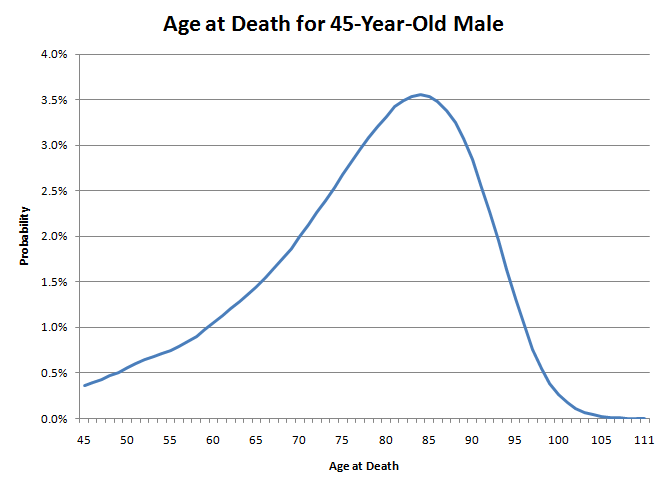
我的死亡年齡就像向這張圖投擲飛鏢一樣。注意左尾比右尾粗得多。這意味著我現在死亡的機率很低。然而,隨著年齡的增長,明年死亡的機率會越來越高。例如,對於一個45歲的男性來說,活到46歲的機率相當高,達到99.64%。然而,到了85歲,活到86歲的機率只有89.21%。這就像大自然慢慢地在你的背後捅刀子。起初它可能不會殺死你,但隨著時間的流逝,它殺死你的機率會慢慢增加。然而,一旦你到了七十多歲後期,大自然就會對你不再玩命,開始真正捅刀子。
因此,如果許多45歲的男性向這張圖投擲飛鏢,49.96%的人將在45歲至79歲之間命中,50.04%的人將在80歲至111歲之間命中。然而,幸運地落在圖表右側的那一半人可能活不過80歲。男性一旦達到80歲,預期壽命也只有7.78年。同時,那些不幸活不到80歲的人,許多人的壽命會比80歲短得多。因此,正是大量年輕人的死亡拉低了平均壽命。
對於類似的情況,考慮一個數字為 10、20、30、31、32、33 的骰子。平均值為 26,但擲出大於該值的機率為 2/3。
舉個例子來說明平均值和中位數的不同之處,假設我們在樣本中再增加兩個死亡病例。一個在46歲時死亡,另一個在81歲時死亡。活到80歲的機率保持不變,但45歲時的平均壽命會下降。
這個問題是在我的同伴網站Wizard of Vegas的論壇中提出並討論的。
為什麼賭場要費心列出用一對K分牌五張A的例外情況?這種情況發生的頻率有多高?如果發生,這種例外情況產生影響的機率有多大?
問得好。賭場規則是,五張A分開,低牌出兩張A。例外情況是,如果你能出兩張K,高牌中五張同點牌就保留。我的牌九撲克頁面列出了拉斯維加斯和大西洋城的七種賭場規則,所有規則都包含這個例外。而這兩座城市以外的三家賭場規則則沒有。
拿到四張A、一張Jow和兩張K的機率是25,690,513分之一。假設莊家押莊,這個例外唯一有用的情況是玩家的高牌是四張同點牌或更好的牌。這種情況的機率約為300分之一。兩者同時發生的機率約為76億分之一。
根據內華達州博彩管理委員會的數據,2009 年內華達州共有 306 張牌九撲克賭桌。如果我們慷慨地假設每小時 60 手,每桌兩名玩家,每張賭桌全天候開放,那麼這種例外情況需要 23.7 年才會發生,並對結果產生影響。
所以賭場要求每位牌九撲克荷官記住這個例外,儘管它在遊戲歷史上可能從未對結果產生過影響。我猜想,提出增加這條規則的人,和決定將A2345順子(即所謂的「輪盤」)定為第二大順子的人是同一個人。
需要擲多少次骰子才能有 50/50 的機率擲出至少一個 12 點?
這是機率論史上的經典問題。很多人錯誤地認為答案是 18,因為擲出 12 的機率是 1/36,而 18×(1/36)=50%。然而,依照這個邏輯,擲 36 次得到 12 的機率應該是 100%,這顯然不是。以下是正確答案。設 r 為擲骰次數。擲出非 12 的機率是 35/36。擲 r 次骰子中沒有擲出 12 的機率是 (35/36) r 。因此,我們需要用以下公式解出 r:
(35/36) r = 0.5
對數(35/36) r = 對數(0.5)
r × log(35/36) = log(0.5)
r = log(0.5)/log(35/36)
r = 24.6051
所以沒有一個整數答案。 24次擲骰子擲出12的機率是1-(35/36) 24 = 49.14%。 25次擲骰子擲出12的機率是1-(35/36) 25 = 50.55%。
如果你想押注,比如說你能在25輪擲出12點,或是其他人在24輪中擲不出。無論哪種情況,你都能在均等投注中佔據優勢。
拉斯維加斯一家體育博彩公司公佈的大學橄欖球比賽總分明顯有誤。市場數字是43,但他們開出的賠率是53。所以我押了大約20次小注,每次金額都很少,以免引起注意或影響賠率。不出所料,我贏了。現在我有點擔心要不要把賭注提交給對方付款。賭場拒絕支付是否合理?
我賭10比1你一定會贏,儘管他們可能會先跟你聊幾句。我之所以有些懷疑,是因為體育博彩公司在獲得博彩管理委員會的許可後,可以撤銷明顯錯誤的投注。
「未經主席事先書面批准,博彩公司不得單方面撤銷任何賭注。」—內華達州法規 22.115
雖然根據傳聞證據,這項權利確實存在,但很少被引用。請告訴我發生了什麼事。
P.S.:提問者後來通知我,他很順利地就拿到了報酬。
想像一條無限彈性的橡皮筋,未拉伸時長1公里,以每秒1公里的速度膨脹。接下來,想像橡皮筋的一端有一隻螞蟻。當橡皮筋開始膨脹時,螞蟻以相對於目前位置每秒1公分的速度向另一端爬行。螞蟻最終會到達另一端嗎?如果會,什麼時候?
是的, 100,000 -1秒後就會了。請參閱我的mathproblems.info網站,問題 206,其中有兩個答案。
這個問題是在我的同伴網站Wizard of Vegas的論壇中提出並討論的。


