請問巫師 #261
什麼樣的動態會影響⾜球總分的押注、當球季進⾏當時, 天氣會變壞、還 有更多關於球隊最近表現的資訊?有多容易(或多難)去發現賭盤的錯誤?
為了協助回答這個問題, 我畫出NFL美式⾜球每週的平均得分數, 基於 1983-2009年每個球季。以下的圖表顯⽰其結果。
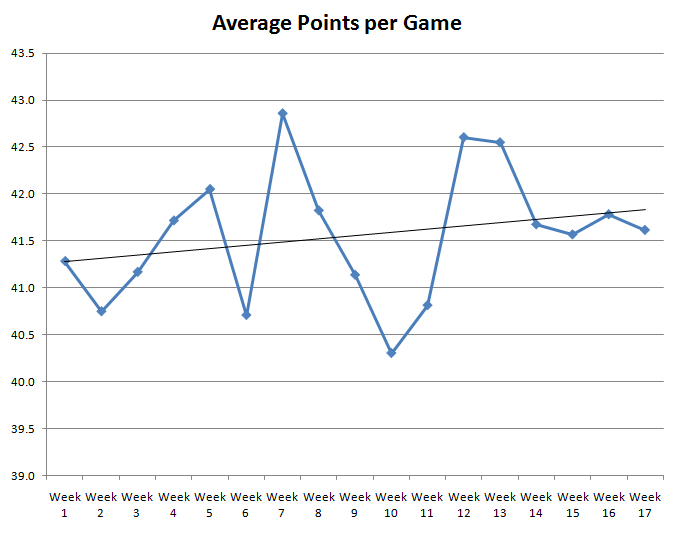
你可以看⾒, 曲線是起起伏伏的。⿊⾊實線是least-squared best fit line最 ⼩平⽅誤差的迴歸線, 總體來說是朝上的趨勢。所以當球季進⾏時, 氣溫下 降, 平均得分漸漸增加, 不過那可能輕易是因為隨機的變化。
這是⺫前為⽌我所能說的。針對天氣影響運動押注的⼀般意⾒, 我轉給我 的朋友Jason Been, 他是這個議題的專家。在這裡他曾說過:
在⼤多數案例, ⾵是天氣最主要影響⽐賽的因素; 不過, 這並⾮唯⼀的⼀項 因素。在棒球與其他的⼾外運動, 陰影可以是相同的效應, 尤其是在球季早 期與晚期的下午⽐賽。下⾬或下雪在⾜球來說、並⾮⼤多數⼈所想的那 般、會是很⼤的因素, 因為同樣都會影響到攻擊與防守的兩⽅。⼀個案例 將會是防守⽅對抗⻑程的接球者。下⾬和下雪將會同樣拖延雙⽅, 因此不 會有哪⼀⽅得到優勢。⾵在⾜球踢球時可以消除傳球的效⼒。我就⾒過⽐ 賽當中, 傳球的⼀⽅被逼著在強勁側⾵當下每次都得要跑著傳球。這並不 常發⽣, 不過⾵的因素最終將會影響到⽐賽的進⾏.這個問題曾被提出與討論在我的夥伴網站討論區 Wizard of Vegas拉斯維 加斯巫師.
如果玩家在玩擲骰子遊戲時下注超過賠率倍數,而莊家直到賭注贏或輸才注意到,通常會發生什麼情況?
我曾就此問題諮詢一位前拉斯維加斯賭桌遊戲經理。他說,賠率投注超過允許的線注倍數的部分將按位置投注賠率支付。這個問題在我的同伴網站“拉斯維加斯巫師”的論壇上被提出並討論過。
在NFL美式⾜球, 平均⽽⾔, ⼀隊得分之後另⼀隊也得分的機率是多少?
根據2000-2009年NFL美式⾜球的球季, 答案是57%.
假設有一場三人決鬥,參與者有A、B和C。他們為了爭奪一個女人而決鬥至死。他們都是紳士,並且都同意以下規則。
- 三位參與者形成一個三角形。
- 每顆子彈只有一顆。
- A 先走,然後 B,最後是 C。
- A 擊中預定目標的機率是 10%。
- B 擊中預定目標的機率為 60%。
- C 擊中預定目標的機率為 90%。
- 沒有發生意外槍擊事件。
- 允許向空中射擊(故意射偏)和射擊自己,並且總是成功的。
- 如果任何一輪結束後仍有兩到三名倖存者,則每人獲得一顆新子彈。之後,他們將按照相同的順序輪流射擊,跳過任何已經死亡的玩家。
- 三位參與者都是完美的邏輯學家。
A 最初應該瞄準誰?他針對每個初始目標的生存機率是多少?
BBC 節目《相當有趣》討論了這個謎題。向下捲動 100 行即可查看答案和解答。
1
2
3
4
5
6
7
8
9
10
11
12
十三
14
15
16
17
18
19
20
21
22
23
24
二十五
二十六
二十七
二十八
二十九
三十
31
三十二
33
三十四
三十五
三十六
三十七
三十八
三十九
40
41
四十二
43
四十四
45
46
四十七
四十八
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
以下是我根據每個初始目標計算出的 A 獲勝的機率。如你所見,故意向空中射擊可以最大化 A 的獲勝機率。
真實賠率
| 策略 | 機率獲勝 |
| 空氣 | 13.887% |
| 一個 | 0.000% |
| B | 12.560% |
| C | 13.094% |
為了解答這個問題,我們用 Pr(X) 表示一輪之後 X 組(且僅剩 X 組)存活的機率。以 Pr(X*) 表示 X 組最終贏得該輪的機率,重複此過程直至遊戲狀態因有人被擊中而改變。以 Pr(X**) 表示玩家 X 是唯一倖存者的機率。為了找到最終的機率,我們先來看看兩人的狀態。顯然,雙方都會向對方射擊。
A 與 B
- Pr(A) = 0.1
- Pr(B) = 0.9×0.6 = 0.54
- Pr(AB) = 0.9×0.4 = 0.36
如果兩人都倖存下來,那麼他們將重複這個過程,直到只剩下一個倖存者。因此,最終倖存者的機率為:
- Pr(A*) = Pr(A)/(1-Pr(AB)) = 0.1/0.64 = 0.15625
- Pr(B*) = Pr(B)/(1-Pr(AB)) = 0.54/0.64 = 0.84375
A 與 C
- Pr(A) = 0.1
- Pr(C) = 0.9×0.9 = 0.81
- Pr(AC) = 0.9×0.1 = 0.09
如果兩人都倖存下來,那麼他們將重複這個過程,直到只剩下一個倖存者。因此,最終倖存者的機率為:
- Pr(A*) = Pr(A)/(1-Pr(AC)) = 0.1/0.91 = 0.10989011
- Pr(C*) = Pr(B)/(1-Pr(AC)) = 0.81/0.91= 0.89010989
B 與 C
- Pr(B) = 0.6
- Pr(C) = 0.4×0.9 = 0.36
- Pr(BC) = 0.$×0.1 = 0.04
如果兩人都倖存下來,那麼他們將重複這個過程,直到只剩下一個倖存者。因此,最終倖存者的機率為:
- Pr(B*) = Pr(A)/(1-Pr(BC)) = 0.6/.96 = 0.625
- Pr(C*) = Pr(B)/(1-Pr(BC)) = 0.36/.96= 0.375
現在我們來分析三人的狀況。我們先來考慮一下 A 瞄準 B 的情況。
三人遊戲-A 瞄準 B
如果A擊中B,那麼C肯定能存活,但可能擊中A,也可能擊不中。因此,擊中B的兩種可能結果是AC和C。如果A擊中B未擊中,那麼B會瞄準威脅更大的C。如果B擊中C,那麼A和B都能存活。如果B擊中C未擊中,那麼C會瞄準威脅更大的B。如果C擊中B未擊中,那麼A和C都能存活。如果C擊中B,那麼A和C都能存活。因此,可能的結果是C、AB、AC和ABC。
- Pr(A) = 0。
- Pr(B) = 0。
- Pr(C) = 0.1 × 0.9 = 0.09。這是透過 A 擊中 B,然後 C 擊中 A 來實現的。
- Pr(AB) = 0.9 × 0.6 = 0.54。這是透過 A 擊中 B,然後 B 擊中 C 來實現的。
- Pr(AC) = 0.1 × 0.1 + 0.9 × 0.4 × 0.9 = 0.334。這可以透過兩種方式實現。第一種是 A 命中 B,然後 C 未命中 A。第二種是 A 未命中 B,B 未命中 C,然後 C 命中 B。
- Pr(BC) = 0。
- Pr(ABC) = 0.9 × 0.4 × 0.1 = 0.036。這是透過三項全部缺失實現的。
按照與雙人情況相同的邏輯,我們可以將每個結果除以 (1-Pr(ABC))=0.964 來找到每個狀態的機率,假設遊戲狀態在回合之後確實發生了變化。
- Pr(C*) = 0.09/0.964 = 0.093361。
- Pr(AB*) = 0.54/0.964 = 0.560166。
- Pr(AC*) = 0.334/0.964 = 0.346473。
從雙人對決的情況來看,如果是A和B,那麼A獲勝的機率為0.15625,B獲勝的機率為0.84375。如果是A和C,那麼A獲勝的機率為0.109890,C獲勝的機率為0.890110。
- Pr(A**) = (0.560165975 × 0.15625) + (0.346473029 × 0.10989011) = 0.125600。 A 可以透過兩種方式獲勝:(1) 進入 AB 狀態,然後獲勝;(2) 進入 AC 狀態,然後獲勝。
- Pr(B**) = 0.560166 × 0.84375 = 0.472640。若B進入AB狀態,則B獲勝,B為勝者。
- Pr(C**) = 0.093361 + (0.346473 × 0.890110) = 0.401760。 C 可以透過 A 殺死 B,然後 C 在第一輪殺死 A 來獲勝,或透過進入狀態 AC,然後 C 獲勝。
因此,如果 A 的策略是先瞄準 B,那麼他成為唯一倖存者的機率是 12.56%。
三人遊戲-A 瞄準 C
如果A擊中C,那麼B肯定會倖存,但可能會擊中A,也可能不會。因此,擊中C的兩種可能結果是AB和B。如果A沒有擊中C,那麼B會瞄準威脅更大的C。如果B擊中C,那麼A和B都會存活。如果B沒有擊中C,那麼C會瞄準威脅更大的B。如果C沒有擊中B,那麼A和B都會存活。如果C擊中B,那麼A和C都會存活。因此,可能的結果是B、AB、AC和ABC。
- Pr(A) = 0。
- Pr(B) = 0.1 × 0.6 = 0.06。
- Pr(C) = 0。
- Pr(AB) = (0.1 × 0.4) + (0.9 × 0.6) = 0.04+0.54 = 0.58。這可以透過兩種方式實現。第一個是 A 擊中 C,然後 B 擊中 A。第二個是 A 擊中 B,然後 B 擊中 C。
- Pr(AC) = 0.9 × 0.4 × 0.9 = 0.324。這是透過 A 缺失 C、B 缺失 C 以及 C 命中 B 來實現的。
- Pr(BC) = 0。
- Pr(ABC) = 0.9 × 0.4 × 0.1 = 0.036。這是透過三項全部缺失實現的。
按照與雙人情況相同的邏輯,我們可以將每個結果除以 (1-Pr(ABC))=0.964 來找到每個狀態的機率,假設遊戲狀態在回合之後確實發生了變化。
- Pr(B*) = 0.06/0.964 = 0.062241。
- Pr(AB*) = 0.58/0.964 = 0.601660。
- Pr(AC*) = 0.324/0.964 = 0.336100。
按照與 A 針對 B 的情況的解決方案相同的邏輯:
- Pr(A**) = (0.601660 × 0.15625) + (0.336100 × 0.10989011) = 0.130943。
- Pr(B**) = 0.062241 + 0.601660 × 0.84375 = 0.569891。
- Pr(C**) = 0.336100 × 0.890110 = 0.299166。
因此,如果 A 的策略是先瞄準 C,那麼他成為唯一倖存者的機率是 13.09%。
三人 — A 故意失手
A故意射偏後,B會瞄準威脅更大的C。如果B擊中C,A和B都會存活。如果B射偏C,C會瞄準威脅更大的B。如果C射偏B,A和B都會存活。如果C射偏B,A和C都會存活。因此,可能的結果是AB、AC和ABC。
- Pr(A) = 0。
- Pr(B) = 0。
- Pr(C) = 0。
- Pr(AB) = 0.6。這是透過 B 擊中 C 來實現的。
- Pr(AC) = 0.4 × 0.9 = 0.36。這是透過 B 未命中 C,然後 C 命中 B 來實現的。
- Pr(BC) = 0。
- Pr(ABC) = 0.4 × 0.1 = 0.04。這是透過全部三個缺失來實現的。
按照與雙人情況相同的邏輯,我們可以將每個結果除以 (1-Pr(ABC))=0.96 來找到每個狀態的機率,假設遊戲狀態在回合之後確實發生了變化。
- Pr(AB*) = 0.6/0.96 = 0.625。
- Pr(AC*) = 0.36/0.96 = 0.375。
按照與 A 針對 B 的情況的解決方案相同的邏輯:
- Pr(A**) = (0.625 × 0.15625) + (0.375 × 0.109890) = 0.138865。
- Pr(B**) = 0.625 × 0.84375 = 0.527344。
- Pr(C**) = 0.375 × 0.890110 = 0.333791。
因此,如果 A 的策略是先瞄準 C,那麼他成為唯一倖存者的機率是 13.89%。
這個問題是在我的同伴網站Wizard of Vegas的論壇中提出並討論的。


