WOO logo

Wizard 巫師推薦

請問巫師 #259

荷蘭有些賭場允許在輪盤賭中使用三重監禁。根據這條規則，等額投注的賭場優勢是多少？我對答案更感興趣。

Maff 來自 England

為了方便其他讀者，在歐洲的許多賭場，如果您在輪盤賭中下了等額賭注，而球落在零上，則該賭注將被凍結。如果下一輪結果導致該賭注獲勝，則該賭注將被退回，且不計獎金。如果球落在相反方向，則該賭注失敗。

如果球落在零上，單次禁注會怎樣？如果賭場只允許單次禁注，那麼它就會輸。然而，有些賭場允許雙次禁注，這就是會發生的情況。如果雙次禁注贏了，它會恢復為單次禁注。如果賭場只允許最多雙次禁注，那麼雙次禁注在另一個零上會輸。同樣的邏輯，如果賭場允許三次禁注，那麼雙次禁注在另一個零上會變成三次禁注。

三重監禁下的賭場優勢是1.370120%。在我解釋如何得出這個結論之前，我們先來比較單重監禁和雙重監禁。假設第一個賭注押在紅色上。

設 Z = 零的機率 = 1/37。
設 R = 紅色數字的機率 = 18/37。

單人監禁

pr（推）= ZR = 0.0131482834。
pr（勝利）= R = 0.4864864865。
pr(損失) = 1-pr(推)-pr(贏) = 0.5003652301。
預期值 = pr(贏)-pr(輸) = -0.0138787436。

雙重監禁

如果第一輪結果為零，玩家將推牌。之後，玩家可以無限次重複 ZR，直到獲得紅色。換句話說，推牌的方式如下：

ZR, Z(ZR)R, Z(ZR)(ZR)R, Z(ZR)(ZR)(ZR)R, ...

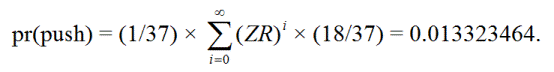
pr（推）= 0.013323464
pr（勝率）= 18/37 = 0.4864864865。
pr(損失) = 1-pr(推)-pr(贏) = 0.5001900494。
預期值 = pr(贏)-pr(輸) = -0.0137035629。

三重監禁

首先，我們來計算一下單註被禁的機率 p 1 ，即單注變成三注，加上兩個零，然後最終又升回單注。這種情況可能發生如下：

ZZRR、ZZ(RZ)RR、ZZ(RZ)(RZ)RR、ZZ(RZ)(RZ)(RZ)RR、...

換句話說，賭注可以在三倍監禁和雙倍監禁之間無限次地反覆。

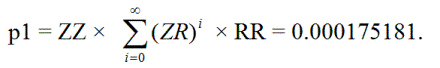
其次，設 p 2 = 單一監禁賭注達到第一級或第二級監禁，然後回到單一監禁的機率。

令 p 2 = ZR + p 1 = 0.013323464。

玩家可以無限次重複返回第一層。因此，平局的機率為：

ZR + Zp2R + Zp2p2R + Zp2p2p2R + ... =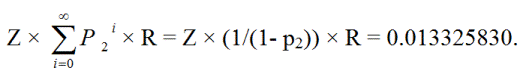

Z × (1/(1- p 2 )) × R = 0.013325830。

pr（推）= 0.013325830。
pr（勝率）= 18/37 = 0.4864864865。
pr(損失) = 1-pr(推)-pr(贏) = 0.5001876839。
預期值 = pr(贏)-pr(輸) = -0.0137011974。

無限期監禁

瑪夫，你沒問，但我聽說西班牙允許無限期監禁。設p=推擠的機率。這也是從x級監禁開始，逐級下降，最後回到x級監禁的機率。

p = ZR + ZpR + ZppR + ZpppR + ...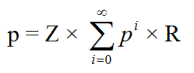

p 2 - p + ZR = 0

根據二次公式 p = (1-(1-4*RZ) 1/2 )/2 = 0.0133258620。

pr（推）= 0.0133258620。
pr（勝率）= 18/37 = 0.4864864865。
pr(損失) = 1-pr(推)-pr(贏) = 0.5001876515。
預期值 = pr(贏)-pr(輸) = -0.0137011650。

Zeros 無視監禁

最後，有些賭場會忽略第一個零之後的零，因為第一個零會限制賭注。在這種情況下，平局的機率就是 (1/37)×(1/2) = 0.0135135135。

下表總結了所有四種規則。

監禁幾率

監禁贏推損失預期的
價值
單身的0.48648649 0.01314828 0.50036523 -0.01387874
雙倍的0.48648649 0.01332346 0.50019005 -0.01370356
三倍0.48648649 0.01332583 0.50018768 -0.01370120
無限0.48648649 0.01332586 0.50018765 -0.01370117
忽略零0.48648649 0.01351351 0.50000000 -0.01351351

我要感謝 ChesterDog 和 weaselman 提供的數學協助。我還要感謝 G. Artico 教授和 polarprof.it 提供上述求和公式的 HTML 程式碼，並在此做個宣傳。

這個問題是在我的同伴網站Wizard of Vegas的論壇中提出並討論的。

請假設以下關於單一視訊撲克機的敘述是正確的。

  • 6-5 獎金撲克累積獎金。
  • 皇家同花順上漲 2%。
  • 5 枚硬幣的遊戲。

現在假設我的情況如下。

  • 最低報酬率為 100.5%。
  • 我有能力玩漸進式遊戲直到它成功。
  • 我知道完美的 6-5 紅利撲克策略，可以獲得 4000 枚硬幣的皇家獎金。

我玩累積獎金的最低限額是多少？

Mark

7,281.8 個金幣。有趣的是，如果你只在這個計量表上玩一次，那麼報酬率只有 98.5%。你應該在這個點玩，是因為你假設你有能力一直玩到中大獎。這就像擁有一個 2% 返現的老虎機俱樂部。 98.5% + 2% = 100.5%。

我想補充一點，如果你在累積獎金剛好達到7,281.8個硬幣時開始使用4,000個硬幣的累積獎金策略，你預期可以獲利201.18個硬幣。但是，如果你花時間學習了7,281.8個硬幣累積獎金的策略變化，那麼你的預期利潤將是234.31個硬幣。

順便提一下，我剛剛讀完了弗蘭克·尼蘭德（Frank Kneeland）的《視頻撲克累積獎金的秘密世界》 。這本書包含許多針對更複雜累積獎金情況的公式，以及他多年管理累積獎金獵人團隊的實踐建議和故事。我推薦給優勢累積獎金視訊撲克玩家。

俄克拉荷馬州一家賭場在六副牌的二十一點牌盒裡放了三張鬼牌。這會對賠率產生什麼影響？

amazed

史丹福‧黃（Stanford Wong）在他的著作《基礎二十一點》（Basic Blackjack）中探討了二十一點中的百搭牌。書中他指出，每副牌中每張百搭牌對玩家來說價值4.2%。因此，每副牌中半張百搭牌的價值為2.1%。書中也介紹了一個策略，根據你的其他牌以及莊家的明牌，決定將哪張牌作為百搭牌。

這個問題是在我的同伴網站Wizard of Vegas的論壇中提出並討論的。

是否有任何調查或數據可以詳細說明拉斯維加斯的二十一點遊戲中有多少百分比是 6-5 或任何其他「嘉年華」類型的變體？

LSUTiger518

根據2010年9月《當代二十一點簡報》的報道，拉斯維加斯共有2099張二十一點賭桌。下表顯示了四種最大二十一點變體的數量。

拉斯維加斯的二十一點變體

遊戲表格百分比
6點到5點467 22.2%
二十一點開關四十二2.0%
超級趣味21 41 2.0%
西班牙 21 6 0.3%
全部的556 26.5%

這個問題是在我的同伴網站Wizard of Vegas的論壇中提出並討論的。