請問巫師 #253
好問題。為了方便其他讀者,以下是雙人遊戲中,這兩手起手牌對抗隨機牌的機率:
KJ 同花 vs. A-7 不同花
| 手 | 贏 | 失去 | 畫 | 預期價值 |
鉀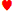 J J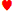 | 0.6148 | 0.3634 | 0.0218 | 0.2513 |
一個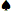 7 7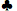 | 0.5717 | 0.3949 | 0.0334 | 0.1768 |
然而,根據我的雙人德州撲克計算器,這兩手牌互相面對的機率是:
A7 勝率 = 53.52%
KJ 勝率 = 46.10%
平手 = 0.39%
所以,在我的牌表中,KJ 同花的排名更高,但在對局中卻不如 A7 異花。為什麼?
答案很難解釋。當兩手牌互相對抗時,你必須考慮它們如何相互作用。例如,在起手牌強度表中,非同花AK僅略優於非同花AQ,預期值分別為0.3064和0.2886。然而,如果將它們互相對抗,AK會壓倒AQ,如下所示:
AK 獲勝率 = 71.72%
AQ 獲勝 = 23.69%
平手 = 4.58%
在A7異花對KJ同花的比賽中,A比K和J高出一籌。 KJ玩家獲勝的最大機會是,他拿到了K或J,並且沒有A出現。我計算出這種情況的機率只有37.73%。其餘46.10%的KJ獲勝機率來自更大的牌。
儘管 A7 對抗 KJ 很強,但它更容易被隨機牌所壓制。
也許這個比喻不太恰當,但它有點像石頭剪刀布遊戲。對於技藝嫻熟的玩家來說,每次出手的力量等級應該大致相同。然而,如果一個玩家出布,另一個出剪刀,那麼力量等級就毫無意義,剪刀會贏。
在拉斯維加斯的 Bighorn and Longhorn 賭場,他們允許在 21 點遊戲中三張牌加倍。根據這條規則,我應該調整策略嗎?
我的「拉斯維加斯巫師」網站的一位讀者說,相對於莊家拿到軟 17 點的標準多副牌策略,應該做出以下改變:
- 擊中軟 13 對抗 5 或 6
- 擊中 2 張軟 15 點對 4 點
- 命中 3,3 對 2
擊中軟牌的原因是,擊中後你可能會得到更好的軟加倍。根據此規則,擊中3的價值更高,因為擊中A可以算作一個好的3張加倍。
這個問題是在我的同伴網站Wizard of Vegas的論壇中提出並討論的。
如果將一枚硬幣拋 100 次,那麼至少有一次連續出現 7 次正面的機率是多少?
我不知道這個問題是否有一個簡單的、非遞歸的表達式來表達。但是,有一個簡單的遞歸表達式來表示。
f(n)= pr(第一次拋反面的個數)×f(n-1) +
pr(第一次拋擲正面,第二次拋擲反面)×f(n-2) +
pr(前兩次拋擲的正面,第三次拋擲的反面)×f(n-3) +
pr(前三次拋擲的正面,第三次拋擲的反面)×f(n-4) +
pr(前四次拋擲的正面,第四次拋擲的反面)×f(n-5) +
pr(前五次拋擲的正面,第五次拋擲的反面)×f(n-6) +
pr(前六次拋擲的正面,第六次拋擲的反面)×f(n-7) +
pr(前 7 次拋擲的正面次數) =
(1/2)×f(n-1)+
(1/2) 2 ×f(n-2)+
(1/2) 3 ×f(n-3)+
(1/2) 4 ×f(n-4)+
(1/2) 5 ×f(n-5)+
(1/2) 6 ×f(n-6)+
(1/2) 7 × f(n-7) +
(1/2) 7
在哪裡:
f(n)=n次翻轉內成功的機率。
pr(x)=x發生的機率。
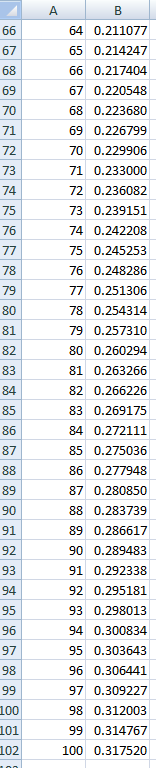
電子表格非常適合解決這類問題。在下面的電子表格截圖中,我在儲存格 B2 到 B8 中輸入了機率 0,因為在 6 次或更少的拋擲次數內不可能連續出現 7 次正面。在儲存格 B9 中,我輸入了以下公式:
=(1/2)*B8+(1/2)^2*B7+(1/2)^3*B6+(1/2)^4*B5+(1/2)^5*B4+(1/2)^6*B3+(1/2)^7*B2+(1/2)^7
然後我把它從單元格B10複製貼上到單元格B102,相當於翻轉100次。這個機率是0.317520。隨機模擬證實了這一點。
 |  |
這篇文章最初發表後,Rick Percy 與我分享了他的矩陣代數解法。以下是我自己的解釋。我假設讀者已經了解矩陣代數的基礎知識。
首先,在任何時候,彈珠台可能處於八種狀態:
p 1 = 成功的機率,假設從當前點開始你需要再擲出 7 個正面。
p 2 = 成功的機率,假設你需要從目前點開始再出現 6 個正面。
p 3 = 成功的機率,假設您需要從當前點開始再出現 5 個正面。
p 4 = 成功的機率,假設您需要從當前點開始再出現 4 個正面。
p 5 = 成功的機率,假設您需要從目前點開始再出現 3 個正面。
p 6 = 成功的機率,假設您需要從當前點開始再出現 2 個正面。
p 7 = 成功的機率,假設您需要從當前點開始再出現 1 個正面。
p 8 = 成功的機率,假設您不需要更多的正面 = 1。
我們將矩陣 S n定義為第 n次翻轉後處於每個狀態的機率。 S 0表示第一次翻轉前的機率,其中有 100% 的機率處於狀態 0。因此 S 0 =
| 1 0 0 0 0 0 0 0 |
設 T 為兩次連續翻轉的變換矩陣,即從 S n到 S n+1 ,其中 S n+1 = T × S n
- 如果您處於狀態 1,那麼在一次翻轉之後,您有 0.5 的機會處於狀態 2(正面),並且有 0.5 的機會保持在狀態 1(反面)。
- 如果您處於狀態 2,那麼在一次翻轉之後,您有 0.5 的機會處於狀態 3(正面),並且有 0.5 的機會返回狀態 1(反面)。
- 如果您處於狀態 3,那麼在一次翻轉之後,您有 0.5 的機會處於狀態 4(正面),並且有 0.5 的機會返回狀態 1(反面)。
- 如果您處於狀態 4,那麼在一次翻轉之後,您有 0.5 的機會處於狀態 5(正面),並且有 0.5 的機會返回狀態 1(反面)。
- 如果您處於狀態 5,那麼在一次翻轉之後,您有 0.5 的機會處於狀態 6(正面),並且有 0.5 的機會返回狀態 1(反面)。
- 如果您處於狀態 6,那麼在一次翻轉之後,您有 0.5 的機會處於狀態 7(正面),並且有 0.5 的機會返回狀態 1(反面)。
- 如果您處於狀態 7,那麼在一次翻轉之後,您有 0.5 的機會處於狀態 8(正面),並且有 0.5 的機會返回狀態 1(反面)。
- 如果您處於狀態 8,那麼您就取得了成功,並且將以 1.0 的機率保持在狀態 8。
將所有這些以轉移矩陣 T = 的形式呈現
| 0.5 0.5 0.0 0.0 0.0 0.0 0.0 0.0 0.0 |
| 0.5 0.0 0.5 0.0 0.0 0.0 0.0 0.0 0.0 |
| 0.5 0.0 0.0 0.5 0.0 0.0 0.0 0.0 0.0 |
| 0.5 0.0 0.0 0.0 0.5 0.0 0.0 0.0 0.0 |
| 0.5 0.0 0.0 0.0 0.0 0.5 0.0 0.0 0.0 |
| 0.5 0.0 0.0 0.0 0.0 0.0 0.5 0.0 0.0 |
| 0.5 0.0 0.0 0.0 0.0 0.0 0.0 0.5 0.0 |
| 0.5 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.5 |
| 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 1.0 |
為了得到一次翻轉後每個狀態的機率...
(1) S1 = S0 ×T
翻轉兩次之後怎麼樣?
(2) S2 = S1 ×T
讓我們用方程式 (2) 來代替方程式 (1)...
(3) S2 = S0 ×T×T= S0 × T2
那麼翻轉 3 次之後呢?
(4) S3 = S2 ×T
將方程式 (3) 代入方程式 (4)...
(5) S3 = S0 × T2 ×T= S0 × T3
我們可以一直這樣做,直到第 100 次翻轉之後的狀態...
S 100 = S 0 × T 100
那麼,T 100是多少呢?在計算機出現之前,要弄清楚這些數字一定非常困難。然而,借助 Excel 的 MMULT 函數,經過大量的複製貼上,我們發現 T 100 =
| 0.342616 0.171999 0.086347 0.043347 0.021761 0.010924 0.005484 0.317520 |
| 0.339863 0.170617 0.085653 0.042999 0.021586 0.010837 0.005440 0.323005 |
| 0.334379 0.167864 0.084271 0.042305 0.021238 0.010662 0.005352 0.333929 |
| 0.323454 0.162380 0.081517 0.040923 0.020544 0.010313 0.005178 0.355690 |
| 0.301693 0.151455 0.076033 0.038170 0.019162 0.009620 0.004829 0.399038 |
| 0.258346 0.129694 0.065109 0.032686 0.016409 0.008237 0.004135 0.485384 |
| 0.171999 0.086347 0.043347 0.021761 0.010924 0.005484 0.002753 0.657384 |
| 0.000000 0.000000 0.000000 0.000000 0.000000 0.000000 0.000000 1.000000 |
右上角的項顯示了翻轉 100 次後處於狀態 8 的機率,即 0.317520。
最近,托斯卡納賭場推出了一項促銷活動:如果你在30天內拿到30張黑傑克,就能贏得100美元的獎金。起初,最低下注金額是5美元,就能在卡上蓋章。後來我聽說最低下注金額提高到了15美元。我給賭場經理寫了一封投訴信,信中寫道:
如果這是真的,我只是想表達我對這個改變的失望。我從來沒有機會利用這個促銷活動,現在也懷疑自己是否還能利用。拿到30張黑傑克所需的時間(據說大約需要連續玩8個小時)似乎不合理,因為促銷活動的獎金仍然只有100美元。
以下是我收到的回覆:
回覆您關於二十一點停牌促銷活動的電子郵件,我不確定您是從哪裡獲得關於完成停牌卡需要多長時間的信息的。我們見過玩家在不到四個小時內就完成了這張卡。而且,您有三十天的時間來完成這張卡。我希望您理解,這並不是一項在這麼短的時間內無法完成的任務。感謝您的來信。很高興收到客戶的回饋。希望您能嘗試並贏得一些獎金!
四小時內拿到 30 張黑傑克的機率是多少?
根據我的遊戲比較,二十一點玩家每小時大約玩70張手牌。六副牌遊戲中出現二十一點的機率是24*96/combin(312,2)=4.75%。我假設二十一點平手仍然會蓋章。所以大約要30/0.0475=632手牌才能填滿牌,也就是9.02小時。
假設玩了280手牌,那麼在4小時內完成牌局的機率是3萬分之一,前提是每次只玩一手牌。我懷疑任何在4小時內達到目標的玩家,每次至少都玩了兩手牌。
這個問題是在我的同伴網站Wizard of Vegas的論壇中提出並討論的。


