請問巫師 #230
今天的新聞是，大西洋城的一名女子在Borgata 賭場連續擲骰子 154 次才擲出 7 點。這意味著她擲了 154 次骰子，沒有一次 7 點。所以我取 (30/36) 154 ，得到的機率超過 1.5 兆分之一。贏得超級百萬彩票的機率比連續擲 154 次非 7 點骰子馬拉鬆的機率高出約 9,000 倍。考慮到這種情況發生的可能性微乎其微，而且人們被定罪的 DNA 證據中虛假匹配的機率只有數十億分之一，您會懷疑作弊嗎？您會就此事諮詢 Borgata 賭場嗎？我已經打電話給他們，告訴他們我的名字，並告訴他們想怎麼處理就怎麼處理。我很想知道您的想法。
首先，她總共擲了 154 次骰子，第 154 次擲出了 7（ 來源：NJ.com ）。但是，這並不意味著她在前 153 次擲骰子中從未擲過 7。她可以在 come out 擲骰子時擲出很多 7。正如我在2003 年 5 月 3 日的專欄中指出的那樣，擲到第 154 次的機率是 56 億分之一。贏得超級百萬大獎的機率是 1 / (56,5)*46 = 175,711,536。因此，擲 154 次或更多的難度大約是 32 倍。如果有足夠的時間和表格（我認為是存在的），這樣的事情遲早會發生。所以，我不會懷疑有人作弊。我粗略估計這種情況在任何一年發生的機率約為 1%。
另請參閱我在mathproblems.info上以矩陣表示的解決方案，問題 204。
Station Casinos 根據賓果遊戲玩家的消費金額，向其提供免費的「Mini X」賓果卡，具體如下：
消費 1-19 美元 = 1 張免費卡
消費 20-29 美元 = 2 張免費卡
消費 30-39 美元 = 3 張免費卡
消費 $40-$49 = 4 張免費卡
消費 50-59 美元 = 5 張免費卡
消費滿 60 美元即可獲得 6 張免費卡
每張卡片上有五個數字，分別對應BINGO中的一個字母。獎品如下：
封面卡上有 5 個數字 = 10,000 美元
6 個數字的封面卡 = 3,000 美元
封面卡上有 7 個數字 = 500 美元
如果沒有人用 7 個或更少的數字覆蓋，則第一個覆蓋的玩家將獲得 50 美元的安慰獎。
下表顯示每張卡的基本獎金價值為 1/5 美分。
Mini X卡的預期價值
| 呼叫 | 支付 | 可能性 | 返回 |
| 5 | 10000 | 0.00000006 | 0.00057939 |
| 6 | 3000 | 0.00000029 | 0.00086909 |
| 7 | 500 | 0.00000087 | 0.00043455 |
| 全部的 | 0.00000122 | 0.00188303 |
每張牌的安慰獎價值為50/n，其中n為參賽牌的數量。例如，如果有1000張參賽牌，那麼每張牌的安慰獎價值為5美分。
在您的視訊撲克雙倍獎金撲克策略頁面上，您聲明如果您得到 5
6 7 8 9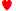
，持有順子是正確的。這對我來說似乎違反直覺，但如果你能更詳細地解釋為什麼持有同花順是一個糟糕的策略，我將不勝感激。
在雙倍獎金遊戲中，同花順賠率為 50，同花賠率為 6，順子賠率為 4。湊成同花順的機率為 2/47，湊成同花的機率為 7/47，湊成順子的機率為 5/47。因此，棄掉 9 的預期回報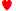為 (2/47)×50 + (7/47)×6 + (5/47)×4 = 3.4468。4 點順子的預期報酬大得多。
拉斯維加斯的 3-5-7 紙牌遊戲怎麼了？我怎麼也找不到。
我聽說這款遊戲因為侵害了專利權，只好從美國賭場下架。根據內華達州博彩管理委員會2008年第四季的統計報告，以下是克拉克縣的賭桌遊戲數量。
克拉克縣桌上遊戲計數
| 遊戲 | 表格 |
|---|---|
| 21 | 2537 |
| 輪盤賭 | 405 |
| 擲骰子 | 334 |
| 其他 | 243 |
| 百家樂 | 233 |
| 三張牌撲克 | 208 |
| 牌九撲克 | 194 |
| 迷你百家樂 | 143 |
| 任逍遙 | 98 |
| 牌九 | 80 |
| 命運之輪（六大） | 三十七 |
| 加勒比海撲克 | 22 |
| 骰寶 | 1 |
| 恰克運氣 | 1 |
不幸的是，他們沒有說明這 243 款「其他」遊戲是什麼，所以這對回答您的問題沒有多大幫助，但仍然值得一提。
先生，我玩了8672場自動單零輪盤遊戲。我預設的號碼竟然出現了278次。我選擇這個號碼是因為口袋的磨損。我怎麼確定這個號碼的機率高於1/37呢？
如果我的術語正確的話，「預測輪盤」是指根據球速、球位置和輪盤速度來預測球的落點。聽起來你的做法是利用偏向性輪盤，這是一種不同的優勢玩法。既然我們討論的是這個話題，那麼第三種優勢玩法就是利用“荷官簽名”，荷官的玩法非常穩定，以至於每次旋轉球和輪盤的速度幾乎都相同。這使得玩家能夠根據球的位置和過往結果來預測球的落點。
回答你的問題，你預期中獎的次數是 8672/37=234.38。變異數是 8672×(1/37)×(36/37)=228.04。標準差是變異數的平方根，即 15.10。你的中獎次數比預期多了 278-234.38=43.62。也就是 (43.62-0.5)/15.10 = 2.8556 個標準差。減去 0.5 的原因很難解釋。簡而言之，這是一個使用連續函數估計離散函數的調整因子。進行高斯近似，中獎次數達到或超過這個數字的機率是 0.21%。所以，你很有可能遇到了一個有偏差的輪盤。然而，仍有 1/466 的可能性，這只是運氣好而已。