請問巫師 #171
別再糾結你的NIM遊戲了!我一直以為獲勝的關鍵在於讓你的對手(這裡指的是電腦)留下的點數加起來等於下一個最小數字,這個數字等於它的二進位總和。也就是說,如果我有17個點,我取2個,剩下15個,也就是二進位數1、2、4、8的總和。但這似乎行不通。我是對還是錯?
你在二進制數上的思路沒錯,但這並非真正的致勝策略。首先,如果你能讓對手留下奇數行,每行一個,那就這樣做。否則,將每一行分解成二進位元素。例如,99 就是 64+32+2+1。然後把所有行上每個元素的數量加起來。最後,尋找一種能讓對手所有行上所有二進位元素數量為偶數的玩法。
我們來看一個例子。假設輪到你了,場景如下。
下表將每一行分解為二進位組件。
玩家第 1 回合
| 排 | 1 | 2 | 4 | 8 | 16 |
| 6 | 0 | 1 | 1 | 0 | 0 |
| 9 | 1 | 0 | 0 | 1 | 0 |
| 4 | 0 | 0 | 1 | 0 | 0 |
| 5 | 1 | 0 | 1 | 0 | 0 |
| 二十五 | 1 | 0 | 0 | 1 | 1 |
| 全部的 | 3 | 1 | 3 | 2 | 1 |
可以看到,1、2、4 和 16 的數量都是奇數。顯然,我們需要讓 25 這一行小於 16,才能消除 16 這個數字。為了讓二進位數字的和保持偶數,我們需要去掉 1,加上 2,加上 4,保留 8,然後去掉 16。這意味著最佳玩法是最後一行 2+4+8=14。保留最後一行 14,我們得到以下結果。
計算機的第一回合
| 排 | 1 | 2 | 4 | 8 | 16 |
| 6 | 0 | 1 | 1 | 0 | 0 |
| 9 | 1 | 0 | 0 | 1 | 0 |
| 4 | 0 | 0 | 1 | 0 | 0 |
| 5 | 1 | 0 | 1 | 0 | 0 |
| 14 | 0 | 1 | 1 | 1 | 0 |
| 全部的 | 2 | 2 | 4 | 2 | 0 |
計算機輪流做事,把這個留給我們。
這是它的二進制分解。
玩家第 2 回合
| 排 | 1 | 2 | 4 | 8 | 16 |
| 6 | 0 | 1 | 1 | 0 | 0 |
| 9 | 1 | 0 | 0 | 1 | 0 |
| 2 | 0 | 1 | 0 | 0 | 0 |
| 5 | 1 | 0 | 1 | 0 | 0 |
| 14 | 0 | 1 | 1 | 1 | 0 |
| 全部的 | 2 | 3 | 3 | 2 | 0 |
這裡我們需要去掉一個 2 和一個 4,才能讓總數相等。只有一行,也就是 14,包含這兩個部分。所以從中去掉 6,剩下 8。
計算機的第二回合
| 排 | 1 | 2 | 4 | 8 | 16 |
| 6 | 0 | 1 | 1 | 0 | 0 |
| 9 | 1 | 0 | 0 | 1 | 0 |
| 2 | 0 | 1 | 0 | 0 | 0 |
| 5 | 1 | 0 | 1 | 0 | 0 |
| 8 | 0 | 0 | 0 | 1 | 0 |
| 全部的 | 2 | 2 | 2 | 2 | 0 |
計算機輪流做事,把這個留給我們。
現在我們需要更改 1、4 和 8 列。
玩家第 3 回合
| 排 | 1 | 2 | 4 | 8 | 16 |
| 6 | 0 | 1 | 1 | 0 | 0 |
| 4 | 0 | 0 | 1 | 0 | 0 |
| 2 | 0 | 1 | 0 | 0 | 0 |
| 5 | 1 | 0 | 1 | 0 | 0 |
| 8 | 0 | 0 | 0 | 1 | 0 |
| 全部的 | 1 | 2 | 3 | 1 | 0 |
可以透過將行 8 更改為 5 來實現,如下所示。
計算機第 3 輪
| 排 | 1 | 2 | 4 | 8 | 16 |
| 6 | 0 | 1 | 1 | 0 | 0 |
| 4 | 0 | 0 | 1 | 0 | 0 |
| 2 | 0 | 1 | 0 | 0 | 0 |
| 5 | 1 | 0 | 1 | 0 | 0 |
| 5 | 1 | 0 | 1 | 0 | 0 |
| 全部的 | 2 | 2 | 4 | 0 | 0 |
計算機輪流做事,把這個留給我們。
現在我們需要更改 2 和 4 的總數。
玩家回合 4
| 排 | 1 | 2 | 4 | 8 | 16 |
| 6 | 0 | 1 | 1 | 0 | 0 |
| 4 | 0 | 0 | 1 | 0 | 0 |
| 2 | 0 | 1 | 0 | 0 | 0 |
| 5 | 1 | 0 | 1 | 0 | 0 |
| 3 | 1 | 1 | 0 | 0 | 0 |
| 全部的 | 2 | 3 | 3 | 0 | 0 |
這可以透過將 6 更改為 0 來實現。
計算機第 4 回合
| 排 | 1 | 2 | 4 | 8 | 16 |
| 0 | 0 | 0 | 0 | 0 | 0 |
| 4 | 0 | 0 | 1 | 0 | 0 |
| 2 | 0 | 1 | 0 | 0 | 0 |
| 5 | 1 | 0 | 1 | 0 | 0 |
| 3 | 1 | 1 | 0 | 0 | 0 |
| 全部的 | 2 | 2 | 2 | 0 | 0 |
計算機輪流做事,把這個留給我們。
現在我們需要改變 2 和 4。
玩家第 5 回合
| 排 | 1 | 2 | 4 | 8 | 16 |
| 0 | 0 | 0 | 0 | 0 | 0 |
| 2 | 0 | 1 | 0 | 0 | 0 |
| 2 | 0 | 1 | 0 | 0 | 0 |
| 5 | 1 | 0 | 1 | 0 | 0 |
| 3 | 1 | 1 | 0 | 0 | 0 |
| 全部的 | 2 | 3 | 1 | 0 | 0 |
這可以透過將 5 行改為 3 行來實現。如果您能讓對手陷入 x,x,y,y 局面,您就必然會獲勝,前提是您可以將相同的局面保持到最後。
計算機的第 5 回合
| 排 | 1 | 2 | 4 | 8 | 16 |
| 0 | 0 | 0 | 0 | 0 | 0 |
| 2 | 0 | 1 | 0 | 0 | 0 |
| 2 | 0 | 1 | 0 | 0 | 0 |
| 3 | 1 | 1 | 0 | 0 | 0 |
| 3 | 1 | 1 | 0 | 0 | 0 |
| 全部的 | 2 | 4 | 0 | 0 | 0 |
接下來的幾步,我讓計算機繼續按照 x,x,y,y 的模式走。這裡計算機給我的結果是 2,2,3,2;所以我留給它的是 2,2,2,2。

然後計算機給了我2,2,1,2。我留下2,2,1,1。
然後計算機給我的結果是2,2,1。我給它留下的是2,2。如果你能把對手的棋子分成兩行,你就贏了,只要保持兩行棋子相等就行了。

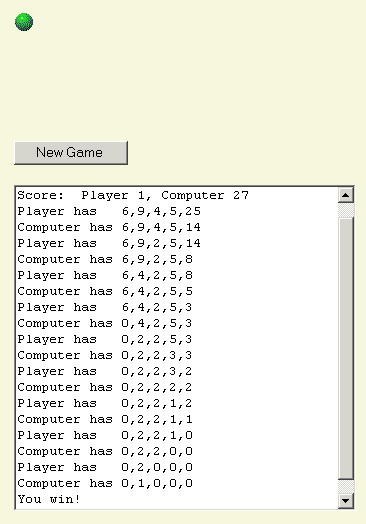
然後計算機給我留下一堆 2,然後我拿走 1。

遊戲到此結束。
我知道當賠率達到或超過10倍時,看跌投注是個不錯的選擇。所以,比如說,如果點數是6或8,就下注5美元,外加50美元的免費賠率。我的問題是,為什麼要等到點數?為什麼不先在過線投注,然後如果點數是6或8,再用10倍的賠率投注呢?這樣你既能獲得賠率優勢,還能在7/11的點數下注。我是不是漏掉了什麼?
我同意。我不建議進行看跌或位置投注,因為正如你所說,賠率線投注比最高賠率投注更高。然而,有些人絕對必須直接投注點數。如果必須這樣做,我建議在位置、買入和看跌之間做出最佳選擇,我會在我的擲骰子部分更詳細地解釋這一點。
我和朋友在拉斯維加斯玩牌。我們大吵了一架,爭論的是,在兩副牌的遊戲中,玩家總點數10,莊家點數7,雙倍下注,還是玩家總點數11,莊家點數10,雙倍下注,哪個從統計上看賠率更高。我以為是前者。
我的二十一點附錄9就是為這類問題設計的。假設有6副牌,我的表格顯示,8+2對7的加倍預期值為0.396342。8+3對10的加倍預期值為0.176919。所以你說得對,10對7的加倍是更好的選擇。
你的網站太棒了,我從中學到了很多。德州撲克翻牌圈,你有20張牌可以讓你贏。為什麼你在河牌圈拿到牌的機率是67.5%,而不是86%(20/47 + 20/46)?我找遍了所有資料,但似乎還是想不通,儘管我知道這大概很簡單。非常感謝你的幫助,謝謝! !
謝謝!你的方法是重複計算你需要的20張牌中的兩張。你在轉牌圈拿到你需要的20張牌中的一張的機率是20/47 = 0.4255。你在轉牌圈沒拿到一張,然後在河牌圈拿到一張的機率是(27/47)*(20/46) = 0.2498。所以總機率是0.4255 + 0.2498 = 0.6753。
我最近在當地部落賭場目睹了一起涉及擲骰子賭桌禮儀的情況,這讓我很困惑,請您幫我解釋一下。玩家「A」在開局擲骰時擲出一個數字,並決定了一個點數。下一輪擲骰時,「A」旁的玩家(玩家「B」)拿起骰子擲出。不清楚他為什麼這麼做,甚至不知道他是否認識「A」。另一位玩家表示反對,指出「B」不是最初的擲骰者。經過荷官和賭桌管理員的一番討論和思考,骰子傳給了下一位玩家(玩家「C」),他最終完成了這局(他最終擲出了7點)。
對於這種情況,這是否是正確的流程?如果是,背後的邏輯是什麼?如果玩家「A」因為某些原因不想再擲骰子,為什麼不允許他放棄骰子?如果玩家「B」因為不懂遊戲規則而拿起骰子,或是發牌員錯誤地將骰子放在他面前,那麼骰子不應該回到「A」手中完成這局遊戲嗎?
我問了nextshooter.com的 Bone Man,他是這樣回答的。
若擲骰者以外的玩家拿起骰子並擲出,則應判為不叫牌、不擲骰,並將骰子交還給正確的擲骰者。雖然這確實是正確的裁決,但在某些情況下,如果結果對所有或大多數玩家有利,賭桌管理員可能會允許擲骰。在某些情況下,擲骰結果可能不會影響任何玩家的投注。另外…任何玩家都可以要求將骰子送給下一位擲骰者以完成一手牌。在這種情況下,可以發送相同的骰子,也可以由新的擲骰者請求新的骰子。擲骰完成後,同一位擲骰者可以擲出自己的手牌,從而擁有多手牌。
擲20個骰子,得到大於100的點數的機率是多少?
我開始使用常態近似來解決這個問題,但超過100個點的機率太低,方法不夠準確。因此,我進行了825萬次試驗的隨機模擬,其中101個點或以上的試驗次數為127次。因此,機率約為65,000分之一。
又到了「一擲千金」的問題了。假設銀行家和席琳狄翁客串演出之後,你只剩下兩個箱子,50萬美元和100萬美元。我猜銀行家的出價會略低於75萬美元。你會選哪一個?如果剩下的兩個箱子分別是0.01美元和100萬美元呢?我想這完全取決於你是不是賭徒,跟賠率沒什麼關係。我問這個問題的原因是,我想知道是否有人能贏得100萬美元(即使他們選的是那個神奇的箱子)。
當獎金金額足以改變人生時,明智的玩家應該謹慎行事,而不是最大化預期價值。一個好的策略應該是最大化預期幸福感。我認為衡量幸福感的一個好函數是你總財富的對數。假設一個人現有財富為 10 萬美元,面臨 0.01 美元和 100 萬美元兩種情況。選擇「不交易」的預期幸福感為 0.5*log(100,000.01 美元) + 0.5*log(1100,000 美元) = 5.520696。設 b 表示玩家無所謂是否接受的銀行報價。
對數(b)= 5.520696
b = 10 5.520696
b = 331,662.50 美元。
所以這位假設的玩家應該會對銀行出價 331,662.50 美元無動於衷。你投入的資金越少,就越應該謹慎行事。通常在遊戲後期,銀行出價接近預期價值,有時甚至會略高一些。玩家贏得百萬美元的唯一合理情況是,他投入了大量資金,並且/或銀行出價異常低廉。製作人似乎喜歡勤奮的中產階級,所以我們不太可能看到有人在涉及大額資金時如此傲慢。我也從未見過銀行在遊戲後期出價低於預期價值 90% 的金額。我們只有在某個無法停止賭博的墮落賭徒出現時才會看到有人贏得百萬美元。當這種情況發生時,我會支持銀行家。
喜歡你的網站!我剛剛看到你列出的拉斯維加斯二十一點賭桌及其優勢的詳細列表,所以我想問一下:假設有兩張二十一點賭桌,一張優勢為0.2%,最低投注額為10美元,另一張優勢為0.4%,最低投注額為5美元。兩張賭桌每手牌的虧損都是0.02美元。選擇其中一張賭桌有什麼優勢嗎?
謝謝。要回答這個問題,你首先得問自己為什麼要賭博。如果你想盡量少輸,那你根本就不該玩。但是,如果你只是為了賭博的樂趣,我建議你選擇10美元、0.2%利潤率的遊戲。預期損失是一樣的,但更大的賭注能讓你獲得更多的滿足感。
尼加拉賭場有一種牌九撲克邊注,賠率不是固定賠率,而是累積獎金。我想知道累積獎金要達到多少才能讓這個賭注收支平衡(假設你把牌局設定為最大化累積獎金的回報)。
損益平衡點是102,680.24美元。我剛剛在我的「牌九撲克邊註」版塊添加了對這個賭注的分析。
我不太懂撲克,但我確實覺得它很有趣,所以也許你可以為我澄清一些事情。最近我和妻子去拉斯維加斯旅行時,我們住在亞利桑那查理迪凱特酒店。我們住在這裡的原因是因為他們在網站上宣傳 2-4 美元的德州撲克遊戲。第一天早上,我們走到撲克室,報名參加 2-4 美元的比賽。我注意到撲克小哥把我們的名字寫在了 4-8 美元的欄位下面。於是我告訴他我們想要 2-4 美元的比賽(同一張紙上有一欄標有“2-4 美元”)。他說是 2-4 美元:翻牌前 2 美元,翻牌後 4 美元,轉牌和河牌後 8 美元。我向他解釋了 2-4 美元的含義:翻牌前和翻牌後都是 2 美元,轉牌和河牌後是 4 美元。他嘲笑我們,好像我們不知道自己在說什麼,並說遊戲不是這樣玩的。我們剩下的旅程都在黃金海岸玩撲克。這種下注方式在撲克室正常嗎? (我最後跟撲克室經理說,如果我們能玩得起4到8美元的德州撲克,我們就不會住在亞利桑那查理賭場了。)
我同意“2/4”遊戲意味著轉牌前下注2美元,轉牌後下注4美元。然而,小盲注很可能是1美元。聽起來,當亞利桑那查理賭場把一局遊戲稱為「2/4」時,他們指的是盲注,這意味著小盲注是2美元,大盲注是4美元,這意味著轉牌後下注8美元。我以前從未聽過這種用法,所以你感到驚訝也就不足為奇了。
P.S.:後來我從撲克室主管安東尼那裡收到了以下內容。
我是一名撲克室管理員。我寫信只是想告訴你德州撲克中撲克限額的正確表述。如果某個遊戲被稱為$2/4,它指的是下注。 (只有在無限注的情況下,遊戲才會以盲注來表示。)翻牌前和翻牌後是$2,轉牌和河牌是$4。如果某個遊戲被列為$2/$4/$8(我猜想上一位寫信人實際上指的是這個,翻牌前是$2,翻牌後是$4,轉牌和河牌是$8)。也可能某個遊戲被列為$2/$4/$6/$8。只要傳遞一下訊息,優秀的撲克室管理員希望人們獲得盡可能多的信息。


