在這一頁
骰寶附錄
在這一頁
簡介
這篇附錄的⺫的是要推導出骰寶賭局中不同押注選項對於玩家的優勢。為 了將事情簡化, 我使⽤玩家的優勢, 有別於賭場的優勢, 因為這樣從玩家的 ⽴場來想事情會⽐較容易些。玩家的優勢總是負數的, 若要得到賭場的優 勢, 只要將之乘以(-1)就好。玩家優勢的通⽤公式是將所有可能的回報率乘 以它們個別的機率。注意丟擲三顆骰⼦總共有6X6X6=216種可能的排列組 合。- 低:
如果不算triple三顆同點的狀況, 這個押注沒有賭場優勢。三顆同點在1點, 2點, 或 3點時的機率為3/216. 總點數在3點到10點之間的機率為1/2, 或 108/216. 所以贏注的機率為 108/216 - 3/216 = 105/216. 因此玩家的優勢 為 (105/216)*(+1) + (111/216)*(-1) = -6/216 =~-2.78%.
- ⾼: 參⾒低
- 特定點數:
搖出0顆骰⼦特定點數的機率為 (5/6)^3 =125/216.
搖出1顆骰⼦特定點數的機率為 3*(1/6)^1*(5/6)^2 = 75/216.
搖出2顆骰⼦特定點數的機率為 3*(1/6)^2*(5/6)^1 = 15/216.
搖出3顆骰⼦特定點數的機率為 (1/6)^3 = 1/216.
因此玩家的優勢為 (125/216)*(-1) + (75/216)*(+1)+ (15/216)*(+2) + (1/216)*(+3) = -17/216 =~-7.780%. - 總點數4點:
共有3種形式搖出4點: (1+1+2, 1+2+1, 2+1+1). 因此玩家的優勢為 3/216*(+60) + (213/216)*(-1) = -33/216 =-15.278%.
- 總點數5點:
共有6種形式搖出5點: (1+1+3, 1+3+1, 3+1+1, 1+2+2, 2+1+2, 2+2+1). 因 此玩家的優勢為 6/216*(+30) + (210/216)*(-1) =-30/216 = -13.889%.
- 總點數6點:
共有10種形式搖出6點: (1+1+4, 1+4+1, 4+1+1, 1+2+3, 1+3+2, 2+1+3, 2+3+1,3+1+2, 3+2+1, 2+2+2). 因此玩家的優勢為 10/216*(+17) + (206/216)*(-1) = -36/216 =-16.667%.
- 總點數7點:
共有15種形式搖出7點: (1+1+5, 1+5+1, 5+1+1, 1+2+4, 1+4+2, 2+1+4, 2+4+1,4+1+2, 4+2+1, 1+3+3, 3+1+3, 3+3+1, 2+2+3, 2+3+2, 3+2+2). 因 此玩家的優勢為 15/216*(+12) + (201/216)*(-1) =-21/216 = -9.722%.
- 總點數8點:
共有21種形式搖出8點: (1-1-6 * 三種, 1-2-5 * 六種, 1-3-4 * 六種, 2-2-4 * 三種, 2-3-3 * 三種). 因此玩家的優勢為 21/216*(+8) + (195/216)*(-1) = -27/216 =-12.500%.
- 總點數9點
共有25種形式搖出9點: (1-2-6 * 六種, 1-3-5 * 六種, 1-4-4 * 三種, 2-2-5 * 三種, 2-3-4 * 六種, 3-3-3 * ⼀種). 因此玩家的優勢為 25/216*(+6) + (191/216)*(-1) =-41/216 = -18.982%.
- 總點數10點:
共有27種形式搖出10點: (1-3-6 * 六種, 1-4-5 * 六種, 2-2-6 * 3 三種, 2-3-5 * 六種, 2-4-4 * 三種, 3-3-4 * 三種). 因此玩家的優勢為 27/216*(+6) + (189/216)*(-1) =-27/216 = -12.500%.
- 總點數11點: 參⾒ 總點數10點
- 總點數12點: 參⾒ 總點數9點
- 總點數13點: 參⾒ 總點數8點
- 總點數14點: 參⾒ 總點數7點
- 總點數15點: 參⾒ 總點數6點
- 總點數16點: 參⾒ 總點數5點
- 總點數17點: 參⾒ 總點數4點
- ⼆數:
讓我們假設所選擇的⼆個點數為1點和2點, 這1點和2點共有30總排列組合: 1-2-1 * 三種, 1-2-2 * 三種,1-2-3 * 六種, 1-2-4 * 六種, 1-2-5 * 六種, 1-2-6 * 六種. 因此玩家的優勢為 30/216*(+5) +(186/216)*(-1) = -36/216 = -16.667%.
- 特三:
只有⼀種⽅式搖出Specific triplet特三的相同點數。因此玩家的優勢為 1/216*(+180) + (215/216)*(-1) = -35/216 =-16.20%.
- 任三:
有6種⽅式搖出Any triplet任三的相同點數。因此玩家的優勢為 6/216*(+30) +(210/216)*(-1) = -30/216 = -13.889%.
- 雙點對⼦:
讓我們假設所選擇的是1點的對⼦, 搖出2顆或3顆1點骰⼦的排列組合共有 16種: 1+1+1, 1+1+2 * 三種, 1+1+3 * 三種, 1+1+4 * 三種, 1+1+5 * 三種, 1+1+6 * 三種. 因此玩家的優勢為 16/216*(+10) + (200/216)*(-1) = -72/216 = -18.52%.
以下為 n 顆骰⼦搖出總點數為 s 的公式, 摘⾃ Richard A. Epstein 所著的 The Theory of Gambling and Statistical Logic 賽局理論與統計邏輯, 公式 5-14.
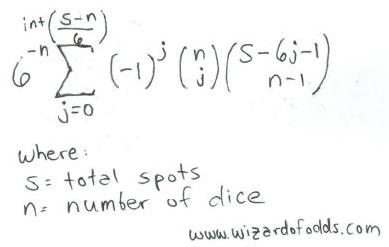
舉例說明, 讓我們以3顆骰⼦搖出點數11為例, 演算如下
int[(s-n)/6] = int[(11-3)/6] = int[1.33] = 1
其總和將是 6-3 * [-10*combin(3,0)*combin(11-6*0-1,3-1) + -11*combin(3,1)*combin(11-6*1-1,3-1) ] =
1/216 * [1*1*combin(10,2) + -1*3*combin(4,2)] =
1/216 * [1*1*45 + -1*3*6] =
1/216 * [45-18] = 27/216 = 12.5%
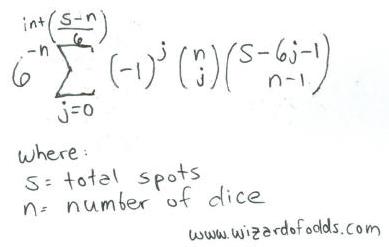











.png)










