在這一頁
押注妙⽅的真相
在這一頁
簡介
「betting systems押注妙⽅」不僅無法擊敗具有賭場優勢的賭場遊戲, 它 們甚⾄不會起到任何⼀點影響。輪盤的⼩球和骰⼦就是沒有記憶, 每次 Roulette輪盤的旋轉和Craps花旗骰的擲骰⼦與過去的所有事件都是獨⽴ 的。在短期間內, 你可以⾃欺地以為某個押注妙⽅是可⾏的、因⽽冒險投 注很多卻贏得很少。然⽽, ⻑期下來沒有任何押注妙⽅是可以禁得起時間 的考驗。你玩的時間愈⻑, 輸掉⾦額相對於押注⾦額的⽐率、將愈加趨近 於那個遊戲的期望值。
經營這個網站多年以來, 我收到過上以千計來⾃押注偏⽅信眾們的e-mails 電郵, 他們的信念已超越了宗教的層次。然⽽, 在所有事情中, 愈是荒謬的 信仰、其信念堅持愈是頑固。數百年來賭徒們就不斷尋求某種可⾏的押注 妙⽅, 然⽽賭場依然屹⽴不搖。
賭徒的謬論
最⼤的賭博神話觀點就是, ⼀個最近都沒發⽣的事件、由於遲遲未發⽣ 過、所以極可能就會發⽣。這就是所謂的「gambler's fallacy賭徒的謬 論」。上千個賭徒曾經設計出押注妙⽅, 嘗試從最近出現的結果、以相反 的押注⽅式來引⽤這款賭徒的謬論。例如, 在輪盤賭桌等待出現三次紅⾊ 之後、再押注在⿊⾊上⾯。⼩販們叫賣「保證」快速發財的押注妙⽅, 最 終就是建⽴在這款賭徒的謬論之上。沒有⼀種妙⽅是有⽤的, 如果你不相 信我的話, 這裡有某些資料來源是說到關於這個主題的:
⼀種普遍的賭徒謬論稱為「機會成熟論」(或「Monte Carlo fallacy蒙地 卡羅謬論」)錯誤地假設在⼀種遊戲之中、每⼀回合的機會並不獨⽴於其 他回合之外, 某⼀種連續結果必然會被另⼀種短缺的機率所平衡。廣泛地 根據這種謬論, 於是賭徒們發明了⼀堆「systems妙⽅」; 賭場經營者樂於 ⿎勵這種妙⽅的使⽤、因為賭徒忽視了機率與獨⽴賭局回合的法則。— Encyclopedia Britannica⼤英百科全書(查看「gambling博弈」條⺫)
沒有押注妙⽅可以將⼀個低於公平的遊戲轉換成獲利的事業... — 《Probability and Measure機率與測量》(第⼆版, 94⾴) by Patrick Billingsley
押注妙⽅「保證」的數字, 關於這種妙⽅的神話與謬誤之擴散, 還有無數⼈ 們成群結黨對於這種妙⽅的相信、傳播、尊崇、保護、和宣誓, 押注妙⽅ 在賭博歷史上建⽴起最古⽼的錯覺。押注妙⽅的狂熱者就像是永動機器擁 護者的精神上親族們, 將他們的頭顱抵擋在熱⼒學第⼆定律之前。 — 《The Theory of Gambling and Statistical Logic博弈與統計邏輯理論》 (53⾴) by Richard A. Epstein
Vegas Click 還有對於賭徒謬論的 ⼀個不錯揭發.
Martingale加倍賭注
我每星期都會收到兩⾄三封電郵, 問我關於輸掉之後加倍賭注的押注妙⽅ 問題。這個⽅法通常是玩在even money⽀付等額注⾦的賭戲上, 例如輪盤 的紅⾊/⿊⾊押注、或是花旗骰的過關/不過關押注, 稱之為「Martingale加 倍賭注」。原理是你每次輸掉之後就加倍賭注, 最終你總會贏⼀局, 不僅回 本了所有輸掉的錢、還倒贏⼀個押注單位的⾦額。例如, 如果玩家從$1開 始玩起、並且連輸四局, 在第五局贏的話, 他在那四局總共輸掉 $1+$2+ $4+$8 = $15, 在第五局贏得$16, 於是輸掉的錢被補償回來、他還獲利 $1. 問題是當你連輸好幾次、押注加倍再加倍很快就會耗光你的賭本, 這可⽐ 你想像中要來得容易。
為了要證明這點, 我創造了⼀個程序來模擬兩種押注⽅式, 「Martingale加 倍賭注」和「flat betting持平押注」兩種⽅式, 並將之運⽤在花旗骰的 pass line過關線押注上(有49.29%贏的機率)。「Martingale加倍賭注」 的押注者總是從押注$1開始玩起, 並且週期開始有$255的資⾦、⾜以連輸 8局。「flat betting持平押注」的押注者則每次只押注$1. 「Martingale加 倍賭注」玩家將玩⾄100局、或是直到他無法負擔押注⾦額為⽌, 在那種情 況時他必須停⽌遊戲、並且帶⾛所剩餘的錢。在他的第100局若是輸的話, 他將繼續押注下去直到贏為⽌、或是直到無法負擔下⼀筆押注賭⾦。 「flat betting持平押注」的玩家則會連玩100局相同的$1押注。我將這兩 種⽅式重複實驗1,000,000個週期、並且將結果製成圖表。以下顯⽰的為 結果:
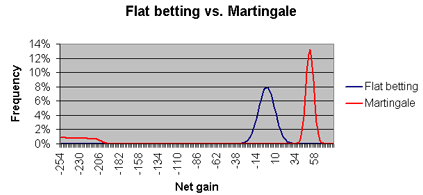
你可以看出, 「flat betting持平押注」的押注者有⼀個鐘形曲線、最⾼峰值 位在輸掉$1的位置, ⽽且不會偏離峰值太遠。通常「Martingale加倍賭 注」的押注者會顯⽰獲利、由最右端的鐘形曲線呈現, 其最⾼峰值位在$51 的位置; 然⽽, 在最左端我們也可⾒到那些因為輸掉⼤量資⾦⽽無法負擔押 注、最後離開的情況。許多加倍賭注的信徒們錯誤地相信, 有較多的贏局 ⾜以補償較少的輸局。
在這個實驗裡, 平均週期的持平押注者輸掉的錢為$1.12, 但加倍押注者輸 掉的錢則為$4.20. 在兩種押注⽅式, 輸掉⾦額相對於押注⾦額的⽐率都⾮ 常接近7/495, 那是花旗骰pass line過關線押注的賭場優勢。這可不是巧 合。不管是⽤什麼押注⽅式, ⻑期下來這個⽐率總是趨近於賭場優勢。為 了證明這點, 考慮「Martingale加倍賭注」的玩家在花旗骰的過關線上只 想贏$1, 從$1開始下注, 並且有資本$2,047 ⾜以連輸10局。以下列表顯⽰ 所有可能結果、機率、期望押注值、還有回報率。
期望押注值expected bet為total bet押注總⾦額乘以機率。同理, 期望回報 率expected return為total return總回報率乘以機率。最後兩個欄位顯⽰加 倍賭注玩家的平均押注總⾦額為11.81172639, 平均輸局為0.16703451. 將 平均輸局除以平均押注⾦額得到0.01414141. 現在我們將7除以495(過關 線的賭場優勢)、我們再次得到0.01414141! 這顯⽰出「Martingale加倍 賭注」相較於「flat betting持平押注」並沒有更好或更糟、若是以期望輸 值expected loss相對於期望押注expected bet的⽐率來看的話。所有的押 注妙⽅若是以這種⽅式相⽐, 則與持平賭注並無不同, 這也本該如此。換⾔ 之, 所有的押注妙⽅都同樣是毫無價值的。
這裡是我稍早之前主導的另⼀個實驗, 證明和上⼀個實驗相同的事。這個 是以三種不同的押注⽅式來測試輪盤賭戲。玩家1每次都持平押注$1, 他 沒有使⽤押注妙⽅。玩家2從$1開始下注, 每次贏錢就再增加$1賭注, 若是 遇到輸局則終⽌增加賭注、回歸到最初押注$1的狀態再從頭開始。玩家3 也是從$1開始下注, 運⽤輸局之後加倍賭注的策略, 也就是輸掉賭注$x之 後他再押注$2x(Martingale加倍賭注), 若是遇到贏局則終⽌加倍賭注、 回歸到最初押注$1的狀態再從頭開始。為了現實的考量, 我將玩家3的最⼤ 押注⾦額限定為$200. 以下是該實驗的結果:
玩家 1
- 總共下注的⾦額 = $1,000,000,000
- 平均下注的⾦額 = $1.00
- 總共輸掉的⾦額 = $52,667,912
- 期待輸掉的⾦額 = $52,667,912
- 輸掉⾦額相對於總下注⾦額的⽐率 = 0.052668
玩家 2
- 總共下注的⾦額 = $1,899,943,349
- 平均下注的⾦額 = $1.90
- 總共輸掉的⾦額 = $100,056,549
- 期待輸掉的⾦額 = $99,997,018
- 輸掉⾦額相對於總下注⾦額的⽐率 = 0.052663
玩家 3
- 總共下注的⾦額 = $5,744,751,450
- 平均下注的⾦額 = $5.74
- 總共輸掉的⾦額 = $302,679,372
- 期待輸掉的⾦額 = $302,355,340
- 輸掉⾦額相對於總下注⾦額的⽐率 = 0.052688
你可以看出, 輸掉⾦額相對於總下注⾦額的⽐率總是接近正常的賭場優勢 1/19 ≈ 0.052632. 隨著之前的輸贏狀況⽽改變押注⾦額的⽅式、和每次總 是押注同等⾦額的⽅式, 在⻑期的結果上並無不同。
第三個實驗
「An Old Timer's Guide to Beating the Craps Table 擊敗花旗骰賭桌的⽼ ⼿指南」曾是⼀種誇⼤保證將花旗骰賭桌變成你的收銀機的⼀種押注妙 ⽅。我免費提供測試他的押注⽅式, 這裡有 結果。
刪除式押注妙⽅
儘管我⼀再警告別⽤押注妙⽅, 讀者們還是不斷來找我尋求建議。為了滿 ⾜這些愛⽤押注妙⽅的⼈們, 我已對這種刪除 式押注妙⽅ 做出全盤的解釋與分析。
別浪費你的錢
網路上充斥著⼀堆販售押注偏⽅的⼈, 允諾可以幸運地在遊戲擊敗賭場。 現今那些販售押注妙⽅的⼈, 就如同19世紀推銷蛇油的江湖郎中。你無論 如何絕對不要浪費錢在任何賭博妙⽅上頭。每次將之放到電腦做出模擬之 後, 肯定會失效、⽽且與「持平押注flat betting」顯⽰出相同的輸錢對押注 的⽐率。如果你問那販賣妙⽅的⼈這個問題, 他可能會回答說:『現實⽣ 活中是沒有⼈會在賭場試驗幾百萬次的。』你也可能聽到他/她的押注⽅ 式在現實⽣活裡可⾏、但⽤在電腦模擬則不⾏。這聽起來倒也有趣, 專業 ⼈⼠利⽤電腦來模擬現實⽣活的問題、幾乎涵括各種領域的研究, 然⽽⼀ 提到押注⽅式的時候, 那販售妙⽅的⼈將之運⽤上去時, 電腦分析就變得 「毫無價值且不可靠」起來。在任何的事件, 這種藉⼝是謬誤的; 電腦試驗 數⼗億次就是為了要證明⼀種押注⽅式是沒有根據的。如果連在電腦上都 ⾏不通的話, 那在賭場也是沒⽤的。
賭博妙⽅伴隨著博弈的歷史⼀樣久遠。沒有任何妙⽅曾被證明過是可⾏ 的。根據內部消息, 我知道販售押注妙⽅的⾏銷者會從販賣這種妙⽅到另 ⼀種妙⽅。這是⼀種骯髒的⾏業, 他們從別⼈那裡盜取想法、並且總是嘗 試改編舊的妙⽅使之看起來像是新的⼀般。
販售妙⽅的⾏銷者通常會允諾荒謬的優勢。例如, 即令押注在even money ⽀付等額注⾦只有1%的優勢, 它也會毫無困難地⼀再疊加押注、從$100 等⽐級數押注達到$1,000,000的資⾦。我曾被要求證明這樣的主張, 所以 寫了⼀個電腦模擬, 以投擲硬幣兩⾯為基礎, 有50.5%贏的機會。整個過程 中玩家押注他資⾦的1%, ⼀元以下四捨五⼊。然⽽, 如果贏局的押注⾦額 超過$1,000,000, 則玩家押注的⾦額只須夠他達到$1,000,000就好。此外, 我還跑了另⼀種模擬、其優勢為2%、起始的資⾦為$1,000. 以下為所有四 種測試的結果。
$100 資⾦, 1% 優勢
- 押注贏 = 7,182,811,698 (50.4999%)
- 押注輸 = 7,040,599,544 (49.5001%)
- 玩家最先達到$1,000,000 = 79,438 (83.019%)
- 玩家最先輸光破產 = 16,249 (16.981%)
- 達到$1,000,000的平均押注局數 = 174,972 (364.5 天, 每天8⼩時, 每⼩ 時押注60局)
$100 資⾦, 2% 優勢
- 押注贏 = 7,027,117,205 (51.0000%)
- 押注輸 = 6,751,539,769 (49.0000%)
- 玩家最先達到$1,000,000 = 215,702 (98.099%)
- 玩家最先輸光破產 = 4,180 (1.901%)
- 達到$1,000,000的平均押注局數 = 63,775 (132.9 天, 每天8⼩時, 每⼩時 押注60局)
$1,000 資⾦, 1% 優勢
- 押注贏 = 5,213,026,190 (50.4999%)
- 押注輸 = 5,109,817,544 (49.5001%)
- 玩家最先達到$1,000,000 = 74,818 (99.0285%)
- 玩家最先輸光破產 = 734 (0.9715%)
- 達到$1,000,000的平均押注局數 = 137,208 (285.8 天, 每天8⼩時, 每⼩ 時押注60局)
$1,000 資⾦, 2% 優勢
- 押注贏 = 6,332,837,070 (50.9996%)
- 押注輸 = 6,084,596,671 (49.0004%)
- 玩家最先達到$1,000,000 = 267,445 (99.9996%)
- 玩家最先輸光破產 = 1 (0.0004%)
- 達到$1,000,000的平均押注局數 = 46,428 (96.7 天, 每天8⼩時, 每⼩時 押注60局)
這些模擬證明了只要⼀點點優勢、像是1%那麼⼩的數值, 還有⼀⼩筆 $100的資⾦, 你就可以⼀路慢慢賭到⼀百萬元、等同於複利計算那樣。但 是你從未聽過這樣的事真實發⽣過。這些賭博⽅式畢竟沒起作⽤嗎?!
這裡有⼀些例⼦是販賣押注妙⽅的銷售者想要欺瞞利⽤數學不佳的⼈。網 路上有好幾百個像這樣的網站, ⽽這個列表只是舉例⽽已。這些網站常常 在⼀夜之間消失、或者突然跳到⾊情網站。如果這些連結並沒有連到指定 的地⽅, 請讓我知道。
還有, ⼩⼼外⾯許多其他販賣迅速致富的賭博騙局, 他們宣稱並⾮是押注妙 ⽅。這些網站通常會弄出⼀堆炫⺫的物理名詞, 像是「Chaos混沌理論」 和「Fractals碎形幾何」, 但⼜顯⽰不出任何證據他們懂得這些字眼的涵 義。過去我曾經列出某些這樣的網站, 但是收到憤怒的來信說道, 我不應該 批評我不懂的事。我個⼈覺得, 每⼀種宣稱可以輕易擊敗賭場的⽅式那就 是詐騙, ⽽且我無須了解箇中的秘密到底為何。然⽽, 為了全然公平起⾒, 我只列舉上述的押注妙⽅, 因為那些在數學上都已經被電腦模擬所破解過 了。如果有⼈真的找到輕易擊敗賭場的⽅式, 那為什麼他們不因此⽽致富 呢?
概率巫師Wizard of Odds挑戰
⼤約有六年的期間, 從1999年到2005年, 我提供$20,000給任何能夠提出⼀ 種押注妙⽅、可以在⼗億次賭局的電腦模擬中顯⽰出獲利。這裡你可以找 到 rules of the challenge挑戰的規則。然⽽, 在整段時期內, 我只有⼀位認 真的挑戰者, 其他幾百⼈都是在浪費我的時間, 假裝有興趣卻從未進⾏到 底。所以在2005年⼀⽉我就將這項獎勵給下架了。
我的版主, Michael Bluejay, 在他⾃⼰的網站 VegasClick.com 現在也提供 本質上相同的挑戰。如果你接受他的挑戰、並且贏了, 我將很樂意在本網 站的⾸⾴宣告, 證明說專家錯了。
第四個實驗
在2004年⼗⽉, Daniel Rainsong接受了我的 挑戰。Rainsong先⽣很有⾃ 信他會贏, 他加倍我的$40,000賭注對抗他的$4,000. 雖然挑戰的規則是基 於Craps花旗骰 或 Roulette輪盤, 我允許這個挑戰可以基於Blackjack⼆⼗ ⼀點的規則、其賭場優勢只有0.26%. ⼀種押注妙⽅可以這麼⼩的賭場優 勢、延展到1,028局押注, 如此去擊敗⼀款遊戲? 請造訪我的挑戰 專⾴查看詳情。
請別再寫信過來了
我對於那些建議玩家如何戰勝負數期望值遊戲的e-mails電郵已經不再回 信了。這樣的電郵只要看到就會被刪除。我在這裡已經把這個主題該說的 都說過了, 還有在我的賭博常問問題集。
如果你真的想要討論這個主題, 那我請你別在我的拉斯維 加斯的巫師 討論區上發⾔, 取⽽代之到志趣相投的⼈們那裡, 像是atJohn Patrick的網站討論區(更新, 這個網站已經, 不意外地, 早就成為過去式 了)。